甲、乙两名篮球运动员在四场比赛中的得分数据以茎叶图记录如下:
| 甲 |
|
乙 |
| |
1 |
8 |
| 6 0 0 |
2 |
4 4 |
| 2 |
3 |
0 |
(Ⅰ)求乙球员得分的平均数和方差;
(Ⅱ)分别从两人得分中随机选取一场的得分,求得分和Y的分布列和数学期望.
(注:方差
其中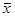 为
为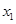 ,
,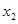 ,
,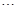
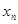 的平均数)
的平均数)
已知函数 ,
, 是都不为零的常数.
是都不为零的常数.
(1)若函数 在
在 上是单调函数,求
上是单调函数,求 满足的条件;
满足的条件;
(2)设函数 ,若
,若 有两个极值点
有两个极值点 ,求实数
,求实数 的取值范围.
的取值范围.
已知椭圆C: 的焦距为4,且与椭圆
的焦距为4,且与椭圆 有相同的离心率,斜率为
有相同的离心率,斜率为 的直线
的直线 经过点M
经过点M
(0,1),与椭圆C交于不同的两点A ,B.
(1)求椭圆C的标准方程;
(2)当椭圆C的右焦点F在以AB为直径的圆内时,求 的取值范围.
的取值范围.
已知函数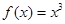
 .
.
(1)求函数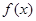 的极值;
的极值;
(2)当 时,求
时,求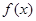 的最值.
的最值.
已知抛物线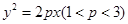 的焦点为
的焦点为 ,抛物线上的点
,抛物线上的点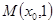 到准线的距离为
到准线的距离为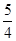 .
.
(1)求抛物线的标准方程;
(2)设直线 与抛物线的另一交点为
与抛物线的另一交点为 ,求
,求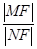 的值.
的值.
已知圆 过点
过点 ,且圆心
,且圆心 在直线
在直线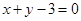 上.
上.
(1)求圆 的方程;
的方程;
(2)若直线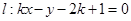 与圆
与圆 交于
交于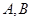 两点,当
两点,当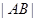 最小时,求直线
最小时,求直线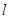 的方程及
的方程及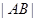 的最小值.
的最小值.