已知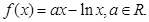
(Ⅰ)当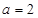 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)若 在
在 处有极值,求
处有极值,求 的单调递增区间;
的单调递增区间;
(Ⅲ)是否存在实数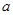 ,使
,使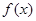 在区间
在区间 的最小值是3,若存在,求出
的最小值是3,若存在,求出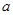 的值;
的值;
若不存在,说明理由.
(本小题满分12分)已知点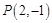 .
.
(Ⅰ)直线 经过点
经过点 ,且在两坐标轴上的截距相等,求直线
,且在两坐标轴上的截距相等,求直线 的方程;
的方程;
(Ⅱ)直线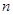 经过点
经过点 ,且坐标原点到该直线的距离为2,求直线
,且坐标原点到该直线的距离为2,求直线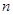 的方程
的方程
(本小题满分12分)已知公差大于零的等差数列 满足:
满足: .
.
(Ⅰ)求数列 通项公式;
通项公式;
(Ⅱ)记 ,求数列
,求数列 的前
的前 项和
项和 .
.
定义:称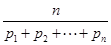 为
为 个正数
个正数 的“均倒数”.已知数列
的“均倒数”.已知数列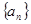 的前
的前 项的“均倒数”为
项的“均倒数”为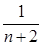 ,
,
(1)求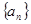 的通项公式;
的通项公式;
(2)设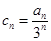 ,试判断并说明数列
,试判断并说明数列 的单调性;
的单调性;
(3)求数列 的前n项和
的前n项和 .
.
已知向量
(1)当 时,求
时,求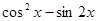 的值;
的值;
(2)设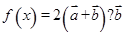 ,已知在
,已知在 中,三个内角A、B、C所对的边分别是
中,三个内角A、B、C所对的边分别是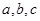 ,若
,若 ,设
,设 ,求
,求 的取值范围.
的取值范围.
已知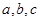 分别是
分别是 三内角A、B、C所对的边,
三内角A、B、C所对的边,
(1)求角A的大小;
(2)若等差数列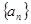 中,
中,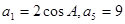 ,设数列
,设数列 的前
的前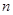 项和为
项和为 ,求证:
,求证: .
.