设函数
(1)当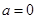 时,求
时,求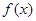 的极值;
的极值;
(2)当 时,求
时,求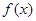 的单调区间;
的单调区间;
(3)当 时,对任意的正整数
时,对任意的正整数 ,在区间
,在区间 上总有
上总有 个数使得
个数使得 成立,试求正整数
成立,试求正整数 的最大值。
的最大值。
如图,三棱锥P—ABC中, 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD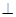 平面PAB。
平面PAB。
(1)求证: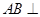 平面PCB;
平面PCB;
(2)求二面角C—PA—B的余弦值。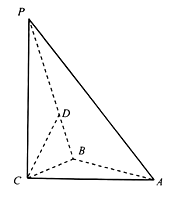
已知函数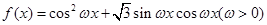 的最小正周期为
的最小正周期为
(1)求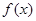 的单调递增区间;
的单调递增区间;
(2)在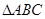 中,a、b、c分别是角A、B、C的对边,若
中,a、b、c分别是角A、B、C的对边,若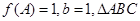 的面积为
的面积为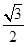 ,求a的值。
,求a的值。
已知:函数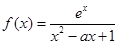 .(其中e为自然对数的底数,e=2.71828…〉.
.(其中e为自然对数的底数,e=2.71828…〉.
(1) 当 时,求函数
时,求函数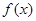 的图
的图 象在点
象在点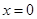 处的切线方程;
处的切线方程;
(2) 当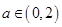 时,试求函数
时,试求函数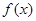 的极值;
的极值;
(3)若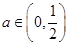 ,则当
,则当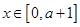 时,函数
时,函数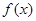 的图象是否总在不等式
的图象是否总在不等式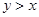 所表示的平面区域内,请写出判
所表示的平面区域内,请写出判 断过程.
断过程.
已知椭圆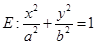 的右焦点为
的右焦点为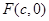 且
且 ,设短轴的一个端点为
,设短轴的一个端点为 ,原点
,原点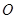 到直线
到直线 的距离为
的距离为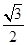 ,过原点和
,过原点和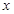 轴不重合的直线与椭圆
轴不重合的直线与椭圆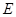 相交于
相交于 两点,且
两点,且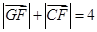 .
.
(1) 求椭圆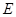 的方程;
的方程;
(2) 是否存在过点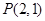 的直线
的直线 与椭圆
与椭圆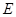 相交于不同的两点
相交于不同的两点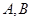 且使得
且使得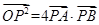 成立?若存在,试求出直线
成立?若存在,试求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
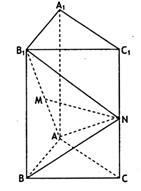
如图,在正三棱柱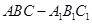 中,
中,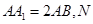 是
是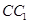 的中点,
的中点, 是线段
是线段 上的动点,且
上的动点,且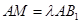
(1)若 ,求证:
,求证: ;
;
(2) 求二面角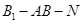 的余弦值;
的余弦值;
(3) 若直线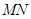 与平面
与平面 所成角的大小为
所成角的大小为 ,求
,求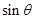 的最大值.
的最大值.