(本小题满分12分)如图,为测得河对岸某建筑物AB的高,先在河岸上选一点C,使C在建筑物底端B的正东方向上,测得点A的仰角为60°,再由点C沿东偏北75°方向走20米到达位置D,测得∠BDC=30°。
(Ⅰ)求sⅠn∠BCD的值;
(Ⅱ)求此建筑物的高度.
(本大题满分12分)定义在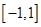 上的函数
上的函数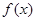 满足:①对任意
满足:①对任意 且
且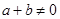 ,都有
,都有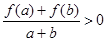 成立; ②
成立; ②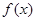 在
在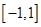 上是奇函数,且
上是奇函数,且 .
.
(1)求证: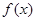 在
在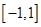 上是单调递增函数;
上是单调递增函数;
(2)解关于 不等式
不等式 ;
;
(3)若 对所有的
对所有的 及
及 恒成立,求实数
恒成立,求实数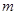 的取值范围.
的取值范围.
(本大题满分12分)如图所示,有一块半径为 的半圆形钢板,设计剪裁成矩形ABCD的形状,它的边
的半圆形钢板,设计剪裁成矩形ABCD的形状,它的边 在圆O的直径上,边CD的端点在圆周上,若设矩形的边
在圆O的直径上,边CD的端点在圆周上,若设矩形的边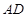 为
为 ;
;
(1)将矩形的面积 表示为关于
表示为关于 的函数,并求其定义域;
的函数,并求其定义域;
(2)求矩形面积的最大值及此时边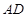 的长度.
的长度.
(本大题满分12分)已知函数 ;
;
(1)求函数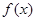 的定义域;
的定义域;
(2)试判断函数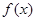 的奇偶性并证明;
的奇偶性并证明;
(3)若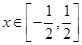 ,求函数
,求函数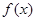 的值域.
的值域.
(本大题满分12分)已知集合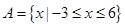 ,
,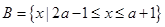 ;
;
(1)若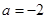 ,求
,求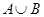 ;
;
(2)若 ,求实数
,求实数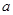 的取值范围.
的取值范围.
(本大题满分10分)已知函数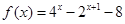 ;
;
(1)求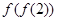 的值;
的值;
(2)若 ,求
,求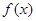 的最大值和最小值.
的最大值和最小值.