在平面直角坐标系
中,已知直线
被圆
截得的弦长为
.
（1）求圆
的方程；
（2）设圆和
轴相交于
，
两点，点
为圆上不同于，的任意一点，直线
，
交
轴于
，
两点．当点变化时，以
为直径的圆
是否经过圆内一定点？请证明你的结论；
（3）若
的顶点
在直线
上，
，
在圆上，且直线
过圆心，
，求点的纵坐标的范围．
如图，在底面是矩形的四棱锥
中，
底面
，
分
别是
的中点，求证：
（1）
平面
；
（2）平面
平面
．
某市在进行城市环境建设中，要把一
个三角形的区域改造成市内公园. 经过测量得到这个
三角形区域的三条边长分别为
(不要求进行近似计算)
（1）求该三角形最大角的余弦值；
（2）求该三角形的面积. 
本题满分7分）已知关于
的不等式
（1）当
时，解该不等式
（2）若不等式对一切实数恒成立，求
的取值范围.
若S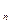
是公差不为0的等差数列
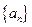的前n项和，且
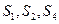成等比数列。
(1)求等比数列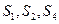的公比； (2)若
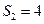，求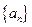的通项公式；
（3）设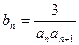
，
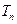是数列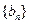
的前n项和，求使得
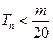对所有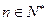
都成立的最小正整数m。
的图象的一部分如下图所示．
的解析式；
的最大值与最小值．