在平面直角坐标系
中,已知直线
被圆
截得的弦长为
.
（1）求圆
的方程；
（2）设圆和
轴相交于
，
两点，点
为圆上不同于，的任意一点，直线
，
交
轴于
，
两点．当点变化时，以
为直径的圆
是否经过圆内一定点？请证明你的结论；
（3）若
的顶点
在直线
上，
，
在圆上，且直线
过圆心，
，求点的纵坐标的范围．
在正四棱柱ABCD－A1B1C1D1中，E为CC1的中点．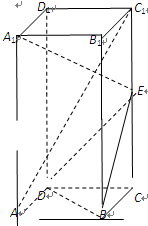
（1）求证：AC1∥平面BDE；（2）求异面直线A1E与BD所成角。
求过直线2x+3y+5=O和直线2x+5y+7=0的交点，且与直线x+3y=0平行的直线的方程，并求这两条平行线间的距离。
已知函数
在定义域
上为增函数，且满足
(1)求
的值 (2)解不等式
设集合P={1，2，3}和Q={－1，1，2，3，4}，分别从集合P和Q中随机取一个数作为
和
组成数对（
,并构成函数
（Ⅰ）写出所有可能的数对(，并计算
，且
的概率；
（Ⅱ）求函数
在区间[
上是增函数的概率.
为了调查某厂2000名工人生产某种产品的能力，随机抽查了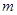
位工人某天生产该产品的数量，产品数量的分组区间为
，
，
,
，
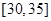,频率分布直方图如图所示．已知生产的产品数量在之间的工人有6位．
（Ⅰ）求；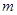
（Ⅱ）工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训，则这2位工人不在同一组的概率是多少？