(本小题10分)
设命题 :对任意实数x,不等式
:对任意实数x,不等式 恒成立;命题
恒成立;命题 :方程
:方程 表示焦点在
表示焦点在 轴上的双曲线.(1)若命题
轴上的双曲线.(1)若命题 为真命题,求实数
为真命题,求实数 的取值范围;(2)若命题:
的取值范围;(2)若命题:  为真命题,且“
为真命题,且“ ”为假命题,求实数m的取值范围.
”为假命题,求实数m的取值范围.
已知 为偶函数,曲线
为偶函数,曲线 过点
过点 ,
,  .
.
(1)若曲线 有斜率为0的切线,求实数
有斜率为0的切线,求实数 的取值范围;
的取值范围;
(2)若当 时函数
时函数 取得极值,确定
取得极值,确定 的单调区间.
的单调区间.
用反证法证明:已知 ,
, ,
, ,求证:
,求证: ,
,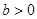 ,
, .
.
已知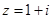 .
.
(1)设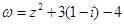 ,求
,求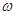 ;
;
(2)如果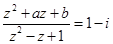 ,求实数
,求实数 的值.
的值.
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.
如图,在△ABC中,B= ,AC=2
,AC=2 ,cosC=
,cosC= .
.
(1)求sin∠BAC的值;
(2)设BC的中点为D,求中线AD的长.