某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶,假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.
(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(2)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向和航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由.
数列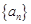 、
、 的每一项都是正数,
的每一项都是正数,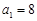 ,
,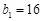 ,且
,且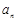 、
、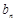 、
、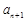 成等差数列,
成等差数列,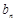 、
、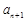 、
、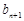 成等比数列,
成等比数列, .
.
(Ⅰ)求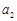 、
、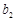 的值;
的值;
(Ⅱ)求数列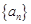 、
、 的通项公式;
的通项公式;
(Ⅲ)记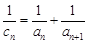 ,证明:对一切正整数
,证明:对一切正整数 ,有
,有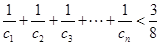 .
.
如图1,矩形 中,
中,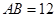 ,
,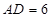 ,
,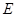 、
、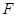 分别为
分别为 、
、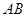 边上的点,且
边上的点,且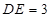 ,
,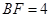 ,将
,将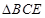 沿
沿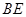 折起至
折起至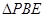 位置(如图2所示),连结
位置(如图2所示),连结 、
、 ,其中
,其中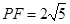 .
.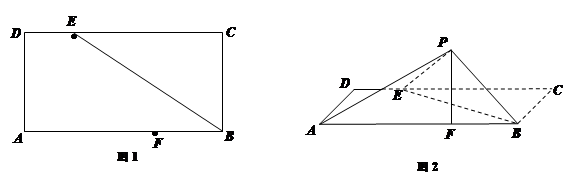
(Ⅰ)求证: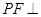 平面
平面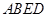 ;
;
(Ⅱ)在线段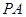 上是否存在点
上是否存在点 使得
使得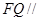 平面
平面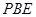 ?若存在,求出点
?若存在,求出点 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
(Ⅲ)求点 到平面
到平面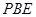 的距离.
的距离.
佛山某中学高三(1)班排球队和篮球队各有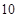 名同学,现测得排球队
名同学,现测得排球队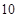 人的身高(单位:
人的身高(单位: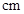 )分别是:
)分别是: 、
、 、
、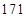 、
、 、
、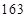 、
、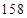 、
、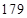 、
、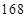 、
、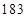 、
、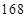 ,篮球队
,篮球队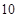 人的身高(单位:
人的身高(单位: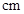 )分别是:
)分别是: 、
、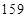 、
、 、
、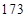 、
、 、
、 、
、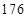 、
、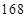 、
、 、
、 .
.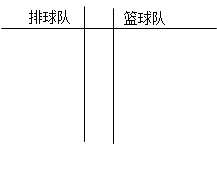
(Ⅰ)请把两队身高数据记录在如图所示的茎叶图中,并指出哪个队的身高数据方差较小(无需计算);
(Ⅱ)现从两队所有身高超过
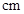 的同学中随机抽取三名同学,则恰好两人来自排球队一人来自篮球队的概率是多少?
的同学中随机抽取三名同学,则恰好两人来自排球队一人来自篮球队的概率是多少?
在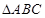 中,角
中,角 、
、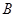 、
、 的对边分别为
的对边分别为 、
、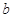 、
、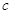 ,且
,且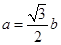 ,
,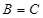 .
.
(Ⅰ)求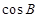 的值;
的值;
(Ⅱ)设函数 ,求
,求 的值.
的值.
设无穷等比数列 的公比为q,且
的公比为q,且 ,
, 表示不超过实数
表示不超过实数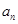 的最大整数(如
的最大整数(如 ),记
),记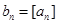 ,数列
,数列 的前
的前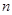 项和为
项和为 ,数列
,数列 的前
的前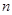 项和为
项和为 .
.
(Ⅰ)若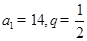 ,求
,求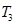 ;
;
(Ⅱ)证明:  (
( )的充分必要条件为
)的充分必要条件为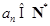 ;
;
(Ⅲ)若对于任意不超过 的正整数n,都有
的正整数n,都有 ,证明:
,证明: .
.