(本小题16分)已知等差数列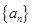 的前
的前 项和为
项和为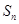 ,且满足
,且满足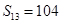 ,公差
,公差 .
.
(1)若 成等比数列,求数列
成等比数列,求数列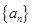 的通项公式;
的通项公式;
(2)是否存在数列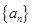 ,使得对任意的
,使得对任意的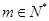 ,
,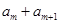 仍然是数列
仍然是数列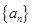 中的一项?若存在,求出所有满足条件的公差
中的一项?若存在,求出所有满足条件的公差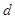 ;若不存在,说明理由;
;若不存在,说明理由;
(3)设数列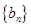 的每一列都是正整数,且
的每一列都是正整数,且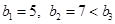 ,若数列
,若数列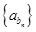 是等比数列,求数列
是等比数列,求数列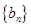 的通项公式.
的通项公式.
在等差数列{ }中,
}中, =3,其前
=3,其前 项和为
项和为 ,等比数列{
,等比数列{ }的各项均为正数,
}的各项均为正数, =1,公比为q,且b2+ S2=12,
=1,公比为q,且b2+ S2=12, .
.
(1)求 与
与 的通项公式;
的通项公式;
(2)设数列{ }满足
}满足 ,求{
,求{ }的前n项和
}的前n项和 .
.
对某市工薪阶层关于“楼市限购政策”的态度进行调查,随机抽查了50人,他们月收入(单位:百元)的频数分布及对“楼市限购政策”赞成人数如下表:
| 月收入(单位百元) |
[15,25 |
[25,35 |
[35,45 |
[45,55 |
[55,65 |
[65,75 |
| 频数 |
5 |
10 |
15 |
10 |
5 |
5 |
| 赞成人数 |
4 |
8 |
12 |
5 |
2 |
1 |
(Ⅰ)根据以上统计数据填写下面2×2列联表,并回答是否有99%的把握认为月收入以5500元为分界点对“楼市限购政策” 的态度有差异?
| 月收入不低于55百元的人数 |
月收入低于55百元的人数 |
合计 |
|
| 赞成 |
 3 3 |
 |
|
| 不赞成 |
 |
 11 11 |
|
| 合计 |
50 |
(Ⅱ)若从月收入在[55,65)的被调查对象中随机选取两人进行调查,求至少有一人赞成“楼市限购政策”的概率.
(参考公式: ,其中
,其中 .)
.)
参考值表:
P( ) ) |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
△ABC中,角A,B,C所对的边分别为 且满足
且满足
(Ⅰ)求角C的大小;
(Ⅱ)求 的最大值,并求取得最大值时
的最大值,并求取得最大值时 的大小.
的大小.
已知函数 .
.
(1)求 的单调区间;
的单调区间;
(2)当 时,若方程
时,若方程 有两个不同的实根
有两个不同的实根 和
和 ,
,
(ⅰ)求实数 的取值范围;
的取值范围;
(ⅱ)求证: .
.
已知椭圆
 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切.
(1)求椭圆 的方程;
的方程;
(2)若过点 (2,0)的直线与椭圆
(2,0)的直线与椭圆 相交于两点
相交于两点 ,设
,设 为椭圆上一点,且满足
为椭圆上一点,且满足 (
( 为坐标原点),求实数
为坐标原点),求实数 取值范围.
取值范围.