(本小题12分).如图,矩形 的顶点
的顶点 为原点,
为原点, 边所在直线的方程为
边所在直线的方程为 ,顶点
,顶点 的纵坐标为
的纵坐标为 .
.
(1)求 边所在直线的方程;
边所在直线的方程;
(2)求矩形 的面积.
的面积.
四边形
的内角
与
互补,
.
(1)求
和
;
(2)求四边形
的面积.
设函数
,记
的解集为
,
的解集为
.
(1)求
;
(2)当
时,证明:
.
将圆
上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线
.
(1)写出
的参数方程;
(2)设直线
与
的交点为
,以坐标原点为极点,
轴正半轴为极坐标建立极坐标系,求过线段
的中点且与
垂直的直线的极坐标方程.
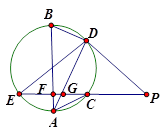
如图, 交圆于 、 两点, 切圆于 为 上一点且 ,连接 并延长交圆于点 ,作弦 垂直 ,垂足为 .
(1)求证:
为圆的直径;
(2)若
,求证:
.
已知函数 , .证明:
(1)存在唯一
,使
;
(2)存在唯一
,使
,且对(1)中的
.