(本小题满分13分)
如图,已知椭圆 :
: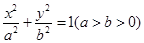 的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)过点 (4,0)且不与坐标轴垂直的直线
(4,0)且不与坐标轴垂直的直线 交椭圆
交椭圆 于
于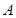 、
、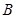 两点,设点
两点,设点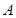 关于
关于 轴的对称点为
轴的对称点为 .
.
(ⅰ)求证:直线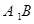 过
过 轴上一定点,并求出此定点坐标;
轴上一定点,并求出此定点坐标;
(ⅱ)求△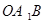 面积的取值范围.
面积的取值范围.
(本小题共13分)在平面直角坐标系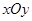 中,设点
中,设点 ,以线段
,以线段 为直径的圆经过原点
为直径的圆经过原点 .
.
(Ⅰ)求动点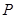 的轨迹
的轨迹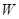 的方程;
的方程;
(Ⅱ)过点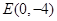 的直线
的直线 与轨迹
与轨迹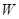 交于两点
交于两点 ,点
,点 关于
关于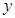 轴的对称点为
轴的对称点为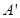 ,试判断直线
,试判断直线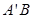 是否恒过一定点,并证明你的结论.
是否恒过一定点,并证明你的结论.
(本小题共14分)已知函数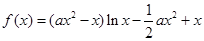 .
. .
.
(Ⅰ)当 时,求曲线
时,求曲线 在
在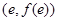 处的切线方程(
处的切线方程(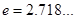 );
);
(Ⅱ)求函数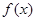 的单调区间.
的单调区间.
(本小题共14分)如图,四棱锥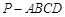 的底面是直角梯形,
的底面是直角梯形,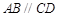 ,
,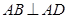 ,
,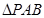 和
和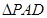 是两个边长为
是两个边长为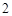 的正三角形,
的正三角形,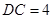 ,
,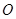 为
为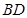 的中点,
的中点,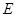 为
为 的中点.
的中点.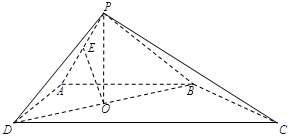
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: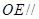 平面
平面 ;
;
(Ⅲ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题共13分)某商场一号电梯从1层出发后可以在2、3、4层停靠.已知该电梯在1层载有4位乘客,假设每位乘客在2、3、4层下电梯是等可能的.
(Ⅰ) 求这4位乘客中至少有一名乘客在第2层下电梯的概率;
(Ⅱ) 用 表示4名乘客在第4层下电梯的人数,求
表示4名乘客在第4层下电梯的人数,求 的分布列和数学期望.
的分布列和数学期望.
(本小题共13分)已知函数
 的最小正周期为
的最小正周期为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求函数 的单调区间及其图象的对称轴方程.
的单调区间及其图象的对称轴方程.