带电量为q=1.0×10-2C的粒子,在电场中先后飞经A、B两点,飞经A点时的动能为EkA=10J,飞经B点时的动能为EkB=40J。已知A点的电势为φA= -700V,粒子只受电场力。求:
(l)粒子从A运动到B的过程中电场力做多少功?
(2)带电粒子在A点的电势能是多少?
(3)B点的电势是多少?
如图甲所示,M和N是相互平行的金属板,OO1O2为中线,O1为板间区域的中点,P是足够大的荧光屏.带电粒子连续地从O点沿OO1方向射入两板间.
(1)若只在两板间加恒定电压U,M和N相距为d,板长为L(不考虑电场边缘效应).若入射粒子是电量为e、质量为m的电子,试求能打在荧光屏P上偏离点O2最远的电子的动能.
(2)若两板间只存在一个以O1点为圆心的圆形匀强磁场区域,磁场方向垂直纸面向里,已知磁感应强度B=0.50T,两板间距d=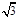 cm,板长L=1.0cm,带电粒子质量m=2.0×10-25kg,电量q=8.0×10-18C,入射速度v =
cm,板长L=1.0cm,带电粒子质量m=2.0×10-25kg,电量q=8.0×10-18C,入射速度v = ×105m/s.若能在荧光屏上观察到亮点,试求粒子在磁场中运动的轨道半径r,并确定磁场区域的半径R应满足的条件.
×105m/s.若能在荧光屏上观察到亮点,试求粒子在磁场中运动的轨道半径r,并确定磁场区域的半径R应满足的条件.
(3)若只在两板间加如图乙所示的交变电压u,M和N相距为d,板长为L(不考虑电场边缘效应).入射粒子是电量为e、质量为m的电子.某电子在t0=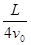 时刻以速度v0射入电场,要使该电子能通过平行金属板,试确定U0应满足的条件.
时刻以速度v0射入电场,要使该电子能通过平行金属板,试确定U0应满足的条件.
(16分)如图所示,足够长的U形导体框架的宽度L=0.5m,电阻可忽略不计,其所在平面与水平面成θ=37°角.有一磁感应强度B=0.8T的匀强磁场,方向垂直于导体框平面.一根质量m=0.2kg、电阻为R=2Ω的导体棒MN垂直跨放在U形框架上,某时刻起将导体棒由静止释放.已知导体棒与框架间的动摩擦因数μ=0.5.(已知sin37°=0.6,cos37°=0.8,g=10m/s2) 
(1)求导体棒刚开始下滑时的加速度的大小.
(2)求导体棒运动过程中的最大速度和重力的最大功率.
(3)从导体棒开始下滑到速度刚达到最大时的过程中,通过导体棒横截面的电量Q=2C,求导体棒在此过程中消耗的电能.
如图所示,质量为m的小物块在光滑的水平面上以v0向右做直线运动,经距离l后,进入半径为R光滑的半圆形轨道,从圆弧的最高点飞出恰好落在出发点上.已知l=1.6m,m=0.10kg,R=0.4m,不计空气阻力,重力加速度g=10m/s2.
(1)求小物块运动到圆形轨道最高点时速度大小和此时小物块对轨道的压力.
(2)求小物块的初速度v0.
(3)若轨道粗糙,则小物块恰能通过圆形轨道最高点.求小物块在这个过程中克服摩擦力所做的功.
雨过天晴,人们常看到天空中出现彩虹,它是由阳光照射到空中弥漫的水珠上时出现的现象.在说明这个现象时,需要分析光线射入水珠后的光路.一细束光线射入水珠,水珠可视为一个半径为R=l0mm的球,球心O到入射光线的垂直距离为d=8mm,水的折射率为n= 4/3.
(a)在图上画出该束光线射入水珠后,第一次从水珠中射出的光路图.
(b)求这束光线从射向水珠到第一次射出水珠,光线偏转的角度.
用油膜法可粗略测出阿伏加德罗常数,把密度ρ=0.8×103 kg/m3的某种油,用滴管滴出一滴油在水面上形成油膜,已知这滴油的体积V=0.5×10-3 cm3,形成的油膜的面积S="0.7" m2,油的摩尔质量Ml="0.09" kg/mol.若把油膜看成单分子层,每个油分子看成球形,那么:
(a)油分子的直径为多大?
(b)由以上数据可测出的阿伏加德罗常数大约为多少?(保留一位有效数字)