如图，在平面直角坐标系中，直角梯形
的边
落在
轴的正半轴上，且
∥，
，=4，
=6，=8．正方形
的两边分别落在坐标轴上，且它的面积等于直角梯形面积。将正方形沿轴的正半轴平行移动，设它与直角梯形的重叠部分面积为
。（1）分析与计算：
求正方形的边长；（2）操作与求解：
①正方形平行移动过程中，通过操作、观察，试判断（＞0）的变化情况是 ；
| A．逐渐增大 | B．逐渐减少 | C．先增大后减少 | D．先减少后增大 |
②当正方形顶点
移动到点
时，求的值；（3）探究与归纳：
设正方形的顶点向右移动的距离为，求重叠部分面积与的函数关系式。
如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB，于点E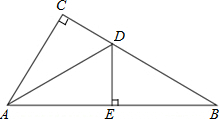
（1）求证：△ACD≌△AED；
（2）若∠B=30°，CD=1，求BD的长。
化简：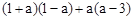
计算：
；
如图，在平面直角坐标系中，直线AB与x轴，y轴分别交于点A（6，0），B（0，8），点C的坐标为（0，m），过点C作CE⊥AB于点E，点D为x轴上一动点，连结CD，DE，以CD，DE为边作□CDEF。
（1）当0< m <8时，求CE的长（用含m的代数式表示）；
（2）当m =3时，是否存在点D，使□CDEF的顶点F恰好落在y轴上？若存在，求出点D的坐标；若不存在，请说明理由；
（3）点D在整个运动过程中，若存在唯一的位置，使得□CDEF为矩形，请求出所有满足条件的m的值。
某校举办八年级数学素养大赛，比赛共设四个项目：七巧板拼图、趣题巧解、数学应用、魔方复原，每个项目得分都按一定百分比折算后计入总分。下表为甲、乙、丙三位同学的得分情况（单位：分）
| 七巧板拼图 |
趣题巧解 |
数学应用 |
魔方复原 |
|
| 甲 |
66 |
89 |
86 |
68 |
| 乙 |
66 |
60 |
80 |
68 |
| 丙 |
66 |
80 |
90 |
68 |
（1）比赛后，甲猜测七巧板拼图、趣题巧解、数学应用、魔方复原这四项得分分别按10%，40%，20%，30%折算计入总分，根据猜测，求出甲的总分；
（2）本次大赛组委会最后决定，总分为80分以上（包括80分）的学生获一等奖。现获悉乙、丙的总分分别是70分，80分，甲的七巧板拼图、魔方复原两项得分折算后的分数和是20分，问：甲能否获得这次比赛的一等奖？