(14分)如图，抛物线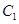
:y＝ax2＋bx+1的顶点坐标为D（1,0），
（1）求抛物线
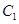的解析式；（2）如图1，将抛物线
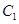向右平移1个单位，向下平移1个单位得到抛物线
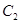，直线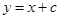
，
经过点D交y轴于点A，交抛物线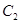于点B，抛物线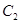的顶点为P,求△DBP的面积； 如图2，连结AP,过点B作BC⊥AP于C,设点Q为抛物线上点
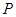至点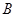
之间的一动点，
连结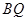 
并延长交
于点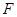
，试问：当点Q运动到什么位置时，△BCF的面积为
。
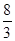一副直角三角板如图放置，点C在FD的延长线上，AB∥CF，∠F=∠ACB=90°，∠E=45°，∠A=60°，AC=10，试求CD的长．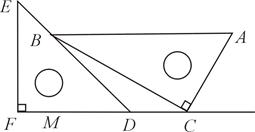
在一只不透明的袋子中，装有2个白球和1个红球，这些球除颜色外都相同。
（1）小明认为，摇匀后从中任意摸出一个球，不是白球就是红球，因此摸出白球和摸出红球是等可能的。你同意他的说法吗？为什么？
（2）摇匀后从中一把摸出两个球，请通过列表或树状图求两个球都是白球的概率；
（3）摇匀后从中任意摸出一个球，要使摸出红球的概率为
，应如何添加红球？
如图，a、b分别代表铁路和公路，点M、N分别代表蔬菜和杂货批发市场。现要建中转站O点，使O点到铁路、公路距离相等，且到两市场距离相等。请用尺规画出O点位置，不写作法，保留痕迹。
请用两种不同的方法解方程：
如图，在平面直角坐标系中，四边形ABCD是平行四边形，AD＝6，若OA、OB的长是关于x的一元二次方程
的两个根，且OA＞OB.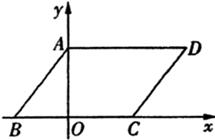
（1）求OA、OB的长；
（2）若点E为x轴上的点，且S△AOE＝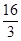
，求经过D、E两点的直线解析式，并判断△AOE与△AOD是否相似；
（3）若点M在平面直角坐标系内，则在直线AB上是否存在点F，使以A、C、F、M为顶点的四边形为菱形？若存在，直接写出F点的坐标，若不存在，请说明理由.