如图,矩形ABCD的边AB="6" cm,BC="8" cm,在BC上取一点P,在CD边上取一点Q,使∠APQ成直角,设BP="x" cm,CQ="y" cm,试以x为自变量,写出y与x的函数关系式.并求 为何值时,
为何值时, 有最大值或最小值?
有最大值或最小值?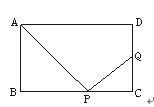
为了满足广大手机用户的需求,某移动通信公司推出了三种套餐,资费标准如下表所示:
| 套餐资费标准 |
|||||||
| 月套餐类型 |
套餐费用 |
套餐包含内容 |
超出套餐后的费用 |
||||
| 本地主叫市话 |
短信 |
国内移动数据流量 |
本地主叫市话 |
短信 |
国内移动数据流量 |
||
| 套餐一 |
18元 |
30分钟 |
100条 |
50兆 |
0.1元/ 分钟 |
0.1元/条 |
0.5元/兆 |
| 套餐二 |
28元 |
50分钟 |
150条 |
100兆 |
|||
| 套餐三 |
38元 |
80分钟 |
200条 |
200兆 |
小莹选择了该移动公司的一种套餐,下面两个统计图都反映了她的手机消费情况.

(1)已知小莹2013年10月套餐外通话费为33.6元,则她选择的上网套餐为________套餐(填“一”、“二”或“三”);
(2)补全条形统计图,并在图中标明相应的数据;
(3)根据2013年后半年每月的消费情况,小莹估计自己每月本地主叫市话通话大约430分钟,发短信大约240条,国内移动数据流量使用量大约为120兆,除此之外不再产生其他费用,则小莹应该选择________套餐最划算(填“一”、“二”或“三”);选择该套餐后,她每月的手机消费总额约为________元.
如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接CF.
(1)求证:四边形ABDF是平行四边形;
(2)若∠CAF=45°,BC=4,CF= ,求△CAF的面积.
,求△CAF的面积.
如图,一次函数 的图象与反比例函数
的图象与反比例函数 的图象交于点
的图象交于点 ,与
,与 轴交于点
轴交于点 .
.
(1)求一次函数的解析式和点 的坐标;
的坐标;
(2)点C在x轴上,连接AC交反比例函数 的图象于点P,且点P恰为线段AC的中点.请直接写出点P和点C的坐标.
的图象于点P,且点P恰为线段AC的中点.请直接写出点P和点C的坐标.
列方程(组)或不等式(组)解应用题:
每年的5月20日是中国学生营养日,某校社会实践小组在这天开展活动,调查快餐营养情况.他们从食品安全监督部门获取了一份快餐的信息(如图).若这份快餐中所含的蛋白质与碳水化合物的质量之和不高于这份快餐总质量的70%,求这份快餐最多含有多少克的蛋白质?
已知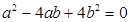 ,
,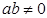 ,求
,求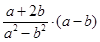 的值.
的值.