某种零件按质量标准分为 五个等级.现从一批该零件中随机抽取
五个等级.现从一批该零件中随机抽取 个,对其等级进行统计分析,得到频率分布表如下:
个,对其等级进行统计分析,得到频率分布表如下:
| 等级 |
 |
 |
 |
 |
 |
| 频率 |
 |
 |
 |
 |
 |
(Ⅰ)在抽取的 个零件中,等级为
个零件中,等级为 的恰有
的恰有 个,求
个,求 ;
;
(Ⅱ)在(Ⅰ)的条件下,从等级为 和
和 的所有零件中,任意抽取
的所有零件中,任意抽取 个,求抽取的
个,求抽取的 个零
个零
件等级恰好相同的概率.
一种电脑屏幕保护画面,只有符号“○”和“×”随机地反复出现,每秒钟变化一次,每次变化只出现“○”和“×”之一,其中出现“○”的概率为p,出现“×”的概率为q,若第k次出现“○”,则记 ;出现“×”,则记
;出现“×”,则记 ,令
,令
(I)当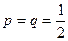 时,记
时,记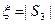 ,求
,求 的分布列及数学期望;
的分布列及数学期望;
(II)当 时,求
时,求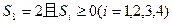 的概率.
的概率.
已知: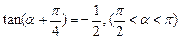 。
。
(1)求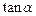 的值;
的值;
(2)求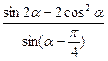 的值。
的值。
已知抛物线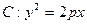 ,点P(-1,0)是其准线与
,点P(-1,0)是其准线与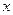 轴的焦点,过P的直线
轴的焦点,过P的直线 与抛物线C交于A、B两点。
与抛物线C交于A、B两点。
(1)当线段AB的中点在直线 上时,求直线
上时,求直线 的方程;
的方程;
(2)设F为抛物线C的焦点,当A为线段PB中点时,求△FAB的面积。
已知集合 ,
,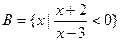
(1)求A B,A
B,A B;
B;
(2)在区间(-4,4)上任取一个实数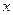 ,求“
,求“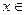 A
A B”的概率;
B”的概率;
(3)设( ,
,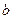 )为有序实数对,其中
)为有序实数对,其中 是从集合A中任意的一个整数,
是从集合A中任意的一个整数,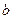 是从集合B中任取一个整数,求“
是从集合B中任取一个整数,求“ A
A B”的概率。
B”的概率。
已知曲线 ,过C上一点
,过C上一点 作斜率
作斜率 的直线,交曲线
的直线,交曲线 于另一点
于另一点 ,再过
,再过 作斜率为
作斜率为 的直线,交曲线C于另一点
的直线,交曲线C于另一点 ,…,过
,…,过 作斜率为
作斜率为 的直线,交曲线C于另一点
的直线,交曲线C于另一点 …,其中
…,其中 ,
,
(1)求 与
与 的关系式;
的关系式;
(2)判断 与2的大小关系,并证明你的结论;
与2的大小关系,并证明你的结论;
(3)求证: .
.