已知命题 :“不等式
:“不等式 对任意
对任意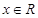 恒成立”,命题
恒成立”,命题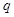 :“方程
:“方程 表示焦点在x轴上的椭圆”,若
表示焦点在x轴上的椭圆”,若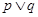 为真命题,
为真命题,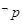 为真,求实数
为真,求实数 的取值范围.
的取值范围.
已知双曲线 的两条渐近线与抛物线
的两条渐近线与抛物线 的准线分别交于A,B两点,O为坐标原点.若双曲线的离心率为2,△AOB的面积为
的准线分别交于A,B两点,O为坐标原点.若双曲线的离心率为2,△AOB的面积为 .
.
(1)求抛物线 的方程;
的方程;
(2)过点 的直线
的直线 与抛物线
与抛物线 交于不同的两点
交于不同的两点 ,若在
,若在 轴上存在一点
轴上存在一点 使得
使得 是等边三角形,求
是等边三角形,求 的值.
的值.
在平面直角坐标系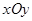 中,已知圆
中,已知圆 :
: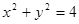 和点
和点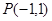 ,过点
,过点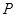 的直线
的直线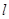 交圆
交圆 于
于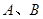 两点.
两点.
(1)若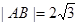 ,求直线
,求直线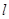 的方程;
的方程;
(2)设弦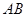 的中点为
的中点为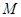 ,求点
,求点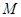 的轨迹方程.
的轨迹方程.
如图,四棱锥P—ABCD的底面为菱形且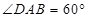 ,PA⊥底面ABCD,AB=2
,PA⊥底面ABCD,AB=2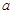 ,PA=
,PA= ,E为PC的中点.
,E为PC的中点.
(1)求直线DE与平面PAC所成角的大小;
(2)求二面角E—AD—C的余弦值.
如图,直三棱柱(侧棱垂直于底面)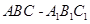 中,
中,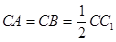 ,点
,点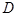 是棱
是棱 的中点,且
的中点,且 .
.
(1)求证: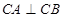 ;
;
(2)求直线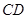 与平面
与平面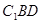 所成角的正弦值.
所成角的正弦值.