已知双曲线 的两条渐近线与抛物线
的两条渐近线与抛物线 的准线分别交于A,B两点,O为坐标原点.若双曲线的离心率为2,△AOB的面积为
的准线分别交于A,B两点,O为坐标原点.若双曲线的离心率为2,△AOB的面积为 .
.
(1)求抛物线 的方程;
的方程;
(2)过点 的直线
的直线 与抛物线
与抛物线 交于不同的两点
交于不同的两点 ,若在
,若在 轴上存在一点
轴上存在一点 使得
使得 是等边三角形,求
是等边三角形,求 的值.
的值.
设函数 ,曲线
,曲线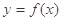 过点P(1,0),且在P点处的切斜线率为2.
过点P(1,0),且在P点处的切斜线率为2.
(1)求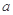 ,
, 的值;
的值;
(2)证明: .
.
某商场销售某种商品的经验表明,该商品每日的销售量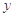 (单位:千克)与销售价格
(单位:千克)与销售价格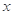 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式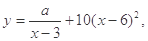 其中
其中 为常数.己知销售价格为5元/千克时,每日可售出该商品11千克.
为常数.己知销售价格为5元/千克时,每日可售出该商品11千克.
(1)求 的值;
的值;
(2)若该商品的成本为3元/千克,试确定销售价格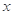 的值,使商场每日销售该商品所获得利润最大.
的值,使商场每日销售该商品所获得利润最大.
设△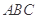 的内角
的内角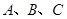 的对边分别为
的对边分别为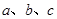 ,且
,且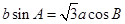 .
.
(1)求角 的大小;
的大小;
(2)若 ,
,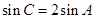 ,求a,c,的值.
,求a,c,的值.
已知函数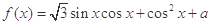 .
.
(1)求 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;
(2)若 在区间
在区间 上的最大值与最小值的和为
上的最大值与最小值的和为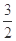 ,求
,求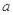 的值.
的值.
m取何实数时,复数
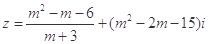 .
.
(1)是实数?
(2)是虚数?
(3)是纯虚数?