(本小题满分14分)
设圆满足:①截y轴所得弦长为2;②被x轴分成两段圆弧,其弧长之比为3:1;③圆心到直线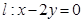 的距离为
的距离为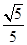 ,求该圆的方程.
,求该圆的方程.
(本小题满分12分)已知f(x)=ax2(a∈R), g(x)="2lnx."
(1)讨论函数F(x)=f(x)-g(x)的单调性;
(2)是否存在实数a,使得f(x)≥g(x)+2 (x>0)恒成立,若不存在,请说明理由;若存在,求出a的取值范围;
(3)若方程f(x)=g(x)在区间 上有两个不相等的实数根,求a的取值范围.
上有两个不相等的实数根,求a的取值范围.
(本小题10分)若函数 ,当
,当 时,函数
时,函数 有极值
有极值 .
.
(1)求函数 的解析式;
的解析式;
(2)若方程 有3个不同的实根,求实数
有3个不同的实根,求实数 的取值范围.
的取值范围.
(本小题8分)机器按照模具生产的产品也会有缺陷,我们将有缺陷的产品称为次品,每小时出现的次品数随机器运转速度的不同而变化.下表为某机器生产过程的数据:
| 速度x(百转/秒) |
2 |
4 |
5 |
6 |
8 |
| 每小时生产次品数y(个) |
30 |
40 |
50 |
60 |
70 |
(1)求机器运转速度与每小时生产的次品数之间的回归方程;
(2)若实际生产所允许的每小时生产的次品数不超过75件,那么机器的速度(百转/秒)不超过多少?(写出满足题目的整数解)
.(本小题8分)已知二次函数 在
在 处取得极值,且在点
处取得极值,且在点 处的切线与直线
处的切线与直线 平行.
平行.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)求函数 在
在 的最值.
的最值.
(本小题8分)全国人民代表大会在北京召开,为了搞好对外宣传工作,会务组选聘了16名男记者和14名女记者担任对外翻译工作.调查发现,男、女记者中分别有10人和6人会俄语.
(1)根据以上数据完成以下 列联表:
列联表:
| 会俄语 |
不会俄语 |
总计 |
|
| 男 |
|||
| 女 |
|||
| 总计 |
(2)能否在犯错的概率不超过0.10的前提下认为性别与会俄语有关?