已知 ,且
,且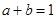 ,求证:
,求证: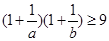
已知圆C的方程为:x2+y2-2mx-2y+4m-4=0.(m∈R).
(1)试求m的值,使圆C的面积最小;
(2)求与满足(1)中条件的圆C相切,且过点(1,-2)的直线方程.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
(1)证明:PF⊥FD;
(2)判断并说明PA上是否存在点G,使得EG∥平面PFD;
(3)若PB与平面ABCD所成的角为45°,求二面角A-PD-F的余弦值.
如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.
(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求二面角C-PB-A的余弦值.
已知一个四棱锥P-ABCD的三视图(正视图与侧视图为直角三角形,俯视图是带有一条对角线的正方形)如图,E是侧棱PC的中点.
(1)求四棱锥P-ABCD的体积;
(2)求证:平面APC⊥平面BDE.
如图,在长方体ABCD-A1B1C1D1中,底面A1B1C1D1是正方形,O是BD的中点,E是棱AA1上任意一点.
(1)证明:BD⊥EC1;
(2)如果AB=2,AE= ,OE⊥EC1,求AA1的长.
,OE⊥EC1,求AA1的长.