问题背景
(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F.请按图示数据填空:
四边形DBFE的面积 ▲ ,
▲ ,
△EFC的面积S1= ▲ ,
△ADE的面积S2= ▲ .
探究发现
(2)在(1)中,若 ,
, ,DE与BC间的距离为
,DE与BC间的距离为 .请证明S2=4S1 S2.
.请证明S2=4S1 S2.
拓展迁移
(3)如图2,平行四边形DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为2、5、3,试利用(2)中的结论求△ABC的面积.
两个布袋中分别装有除颜色外,其他都相同的2个白球,1个黑球,同时从这两个布袋中各摸出一个球,请用树状图表示出可能出现的情况,并求出摸出的两球颜色相同的概率。
计算题
(1) (2)
(2) 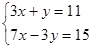
(3)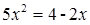 (配方法)(4)
(配方法)(4)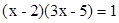 (公式法)
(公式法)
(5)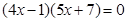 (6)
(6)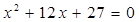
为解决农民工子女入学难的问题,某市建立了进城农民工子女就学的保障机制,其中一项就是免交“借读费”.据统计,2011年秋季有5 000名农民工子女在城区中小学学习,2012年秋季在城区中小学学习的农民工子女比2011年有所增加,其中小学增加20%,中学增加30%,这样,2012年秋季共新增1 160名农民工子女在城区中小学学习.
(1)如果按小学每生每年收“借读费”600元,中学每生每年收“借读费”1 200元计算,2012年新增的1 160名农民工子女共免收多少“借读费”?
(2)如果小学每15名学生配备1名教师,中学每40名学生配备3名教师,若按2012年秋季入学后,农民工子女在城区中小学就读的人数计算,一共需要配备多少名中小学教师?
如图,在长方形ABCD中,AD=BC=16,AB=DC=12,点P和点Q分别是两个运动的点.动点P从A点出发,沿线段AB,BC向C点运动,速度为每秒2个单位长度;动点Q从B点出发,沿线段BC向C点运动,速度为每秒1个单位长度.P,Q同时出发,从两点出发时开始计时,设运动的时间是t(秒).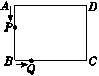
(1)请用含t的代数式表示下面线段的长度;
当点P在AB上运动时,AP=_________;PB=_________;
当点P运动到BC上时,PB=_________;PC=_________;
(2)当点P在AB上运动时,t为何值时,线段PB与线段BQ的长度相等?
(3)当t为何值时,动点P与动点Q在BC边上重合?
某校九年级(1)班所有学生参加2012年初中毕业生升学体育测试,根据测试评分标准,将他们的成绩进行统计后分为A,B,C,D四等,并绘制成如图,如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题: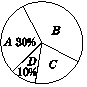

(1)九年级(1)班参加体育测试的学生有_________人;
(2)将条形统计图补充完整;
(3)在扇形统计图中,等级B部分所占的百分比是_____,等级C部分对应的圆心角的度数为_____°;
(4)若该校九年级学生共有850人参加体育测试,估计达到A级和B级的学生共有多少人?