已知某几何体的直观图和三视图如下图所示, 其正视图为矩形,左视图为等腰直角三角形,俯视图为直角梯形.
(1)证明: 平面
平面 ;
;
(2)求二面角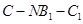 的余弦值;
的余弦值;
(3)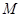 为
为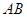 的中点,在线段
的中点,在线段 上是否存在一点
上是否存在一点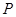 ,使得
,使得 平面
平面 ,若存在,求出
,若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
(本小题满分12分)从含有两件正品 、
、 和一件次品
和一件次品 的3件产品中每次任取一件,连续取两次,求分别在下列两种情况下恰有一件是次品的概率。
的3件产品中每次任取一件,连续取两次,求分别在下列两种情况下恰有一件是次品的概率。
(1)每次取出不放回;
(2)每次取出后放回。
(本小题满分12分)已知 、
、 ,且
,且 。求证:
。求证: 。
。
(本小题满分12分)某射击运动员在一次射击中,命中10环、9环、8环、7环的概率分别为0.2、0.35、0.2、0.15。求此运动员
(1)在一次射击中,命中10环或9环的概率。
(2)在一次射击中,命中环数小于8环的概率。
(3)在两次射击中,至少有一次击中10环的概率。
(本小题满分12分)已知函数 ,输入自变量
,输入自变量 的值,输出对应的函数值
的值,输出对应的函数值 。(1)画出算法框图。(2)写出程序语句。
。(1)画出算法框图。(2)写出程序语句。
(12分)已知函数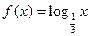 ,
,
(1)当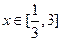 时,求
时,求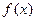 的反函数
的反函数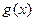 ;
;
(2)求关于 的函数
的函数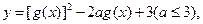 当
当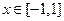 时的最小值
时的最小值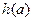 ;
;
(3)我们把同时满足下列两个性质的函数称为“和谐函数”: ①函数在整个定义域上是单调增函数或单调减函数;②在函数的定义域内存在区间
①函数在整个定义域上是单调增函数或单调减函数;②在函数的定义域内存在区间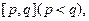 使得函数在区间
使得函数在区间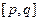 上的值域为
上的值域为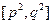 .
. (Ⅰ)判断(2)中
(Ⅰ)判断(2)中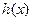 是否为“和谐函数”?若是,求出
是否为“和谐函数”?若是,求出 的值或关系式;若不是,请说明理由;
的值或关系式;若不是,请说明理由;
(Ⅱ)若关于 的函数
的函数 是“和谐函数”,求实数
是“和谐函数”,求实数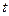 的取值范围.
的取值范围.