(12分)已知函数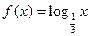 ,
,
(1)当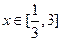 时,求
时,求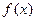 的反函数
的反函数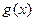 ;
;
(2)求关于 的函数
的函数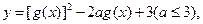 当
当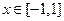 时的最小值
时的最小值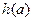 ;
;
(3)我们把同时满足下列两个性质的函数称为“和谐函数”: ①函数在整个定义域上是单调增函数或单调减函数;②在函数的定义域内存在区间
①函数在整个定义域上是单调增函数或单调减函数;②在函数的定义域内存在区间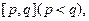 使得函数在区间
使得函数在区间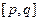 上的值域为
上的值域为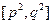 .
. (Ⅰ)判断(2)中
(Ⅰ)判断(2)中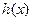 是否为“和谐函数”?若是,求出
是否为“和谐函数”?若是,求出 的值或关系式;若不是,请说明理由;
的值或关系式;若不是,请说明理由;
(Ⅱ)若关于 的函数
的函数 是“和谐函数”,求实数
是“和谐函数”,求实数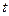 的取值范围.
的取值范围.
数列 满足
满足
 .
.
(Ⅰ)若 是等差数列,求其通项公式;
是等差数列,求其通项公式;
(Ⅱ)若 满足
满足 ,
,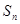 为
为 的前
的前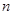 项和,求
项和,求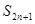 .
.
已知向量  与
与 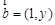 共线,设函数
共线,设函数  。
。
(1)求函数 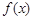 的周期及最大值;
的周期及最大值;
(2)已知锐角 △ABC 中的三个内角分别为 A、B、C,若有  ,边 BC=
,边 BC= ,
,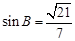 ,求 △ABC 的面积.
,求 △ABC 的面积.
设集合 ,
, .
.
(1)求集合 ;
;
(2)若关于 的不等式
的不等式 的解集是B,求
的解集是B,求 的值.
的值.
设二次函数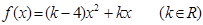 ,对任意实数
,对任意实数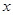 ,
,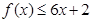 恒成立;正数数列
恒成立;正数数列 满足
满足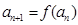 .
.
(1)求函数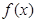 的解析式和值域;
的解析式和值域;
(2)试写出一个区间 ,使得当
,使得当 时,数列
时,数列 在这个区间上是递增数列,并说明理由;
在这个区间上是递增数列,并说明理由;
(3)若已知 ,求证:数列
,求证:数列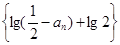 是等比数列
是等比数列
已知函数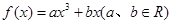 ,当
,当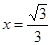 时取极小值
时取极小值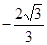 。
。
(1)求 的解析式;
的解析式;
(2)如果直线 与曲线
与曲线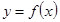 的图象有三个不同的交点,求实数
的图象有三个不同的交点,求实数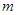 的取值范围。
的取值范围。