如图,过点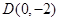 作抛物线
作抛物线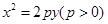 的切线
的切线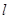 ,切点
,切点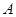 在第二象限.
在第二象限.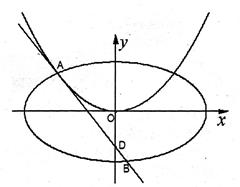
(1)求切点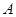 的纵坐标;
的纵坐标;
(2)若离心率为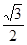 的椭圆
的椭圆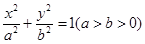 恰好经过切点
恰好经过切点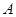 ,设切线
,设切线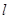 交椭圆的另一点为
交椭圆的另一点为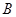 ,记切线
,记切线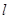 ,
,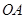 ,
, 的斜率分别为
的斜率分别为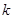 ,
,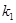 ,
,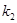 ,若
,若 ,求椭圆方程.
,求椭圆方程.
已知椭圆 的离心率为
的离心率为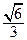 ,过右顶点A的直线l与椭圆C相交于A、B两点,且
,过右顶点A的直线l与椭圆C相交于A、B两点,且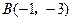 .
.
(1)求椭圆C和直线l的方程;
(2)记曲线C在直线l下方的部分与线段AB所围成的平面区域(含边界)为D.若
曲线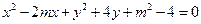 与D有公共点,试求实数m的最小值.
与D有公共点,试求实数m的最小值.
已知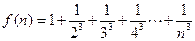 ,
,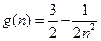 ,
,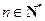 .
.
(1)当 时,试比较
时,试比较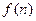 与
与 的大小关系;
的大小关系;
(2)猜想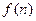 与
与 的大小关系,并给出证明.
的大小关系,并给出证明.
如图①, ,
, 分别是直角三角形
分别是直角三角形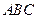 边
边 和
和 的中点,
的中点,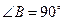 ,沿
,沿 将三角形
将三角形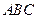 折成如图②所示的锐二面角
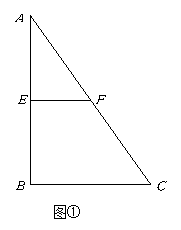
折成如图②所示的锐二面角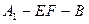 ,若
,若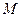 为线段
为线段 中点.求证:
中点.求证:
(1)直线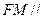 平面
平面 ;
;
(2)平面 平面
平面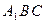 .
.
设函数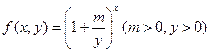 .
.
(1)当 时,求
时,求 的展开式中二项式系数最大的项;
的展开式中二项式系数最大的项;
(2)若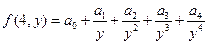 且
且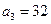 ,求
,求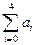 ;
;
某次乒乓球比赛的决赛在甲乙两名选手之间举行,比赛采用五局三胜制,按以往比赛经验,甲胜乙的概率为 .
.
(Ⅰ)求比赛三局甲获胜的概率;
(Ⅱ)求甲获胜的概率;
(Ⅲ)设甲比赛的次数为 ,求
,求 的数学期望.
的数学期望.