(本小题满分7分)选修4—5:不等式选讲
已知a2+b2+c2=1(a,b,c∈ ),求a+b+c的最大值.
),求a+b+c的最大值.
( 本小题满分12分)
设函数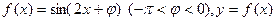 图像的一条对称轴是直线
图像的一条对称轴是直线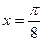
(Ⅰ)求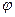 ;
;
(Ⅱ)求函数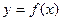 的单调区间及最值;
的单调区间及最值;

(本小题满分12分)
已知函数 是定义在实数集R上的奇函数,函数
是定义在实数集R上的奇函数,函数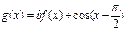 是区间
是区间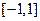 上的减函数。
上的减函数。
(I)求实数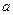 的值;
的值;
(II)若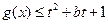 对
对 恒成立,求实数
恒成立,求实数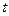 的取值范围;
的取值范围;
(III)讨论关于 的方程
的方程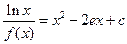 的实根的个数
的实根的个数
本小题满分12分)
已知数列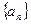 的前n项和为
的前n项和为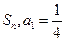 且
且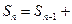
 ,
,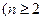 且
且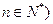 ,数列
,数列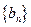 满足
满足 且
且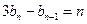
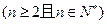 .
.
(I)求数列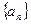 的通项公式;
的通项公式;
(II)求证:数列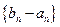 为等比数列;
为等比数列;
(III)求数列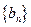 前
前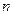 项和的最小值.
项和的最小值.
(本小题满分12分)
已知以向量v=(1, 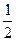 )为方向向量的直线l过点(0,
)为方向向量的直线l过点(0, 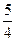 ),抛物线C:
),抛物线C: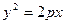 (p>0)的顶点关于直线l的对称点在该抛物的准线上.
(p>0)的顶点关于直线l的对称点在该抛物的准线上.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设A、B是抛物线C上两个动点,过A作平行于x轴的直线m交直线OB于点N,若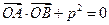 (O为原点,A、B异于原点),试求点N的轨迹方程.
(O为原点,A、B异于原点),试求点N的轨迹方程.