已知函数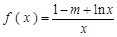 ,
,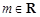 .
.
(Ⅰ)求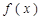 的极值;
的极值;
(Ⅱ)若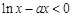 在
在 上恒成立,求
上恒成立,求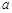 的取值范围.
的取值范围.
(Ⅰ)(Ⅱ)两道题普通班可以任意选择一道解答,实验班必做(Ⅱ)题
(Ⅰ)已知等比数列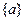 中,
中,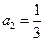 ,公比
,公比 。
。
(1)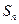 为
为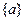 的前
的前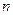 项和,证明:
项和,证明: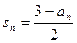
(2)设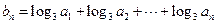 ,求数列
,求数列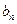 的通项公式.
的通项公式.
(Ⅱ)设正数数列{an}的前n项和为Sn满足Sn= (an+1)
(an+1)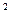 (n∈N*).
(n∈N*).
(1)求出数列{an}的通项公式。
(2)设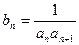 ,记数列{bn}的前n项和为
,记数列{bn}的前n项和为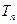 ,求
,求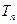
已知函数f(x)=sin(2x-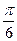 )-1, 设△ABC的内角A、B、C的对边长分别为a、b、c,且c=
)-1, 设△ABC的内角A、B、C的对边长分别为a、b、c,且c=
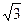 ,f(C)=0,若向量m=(1,sinA)与向量n=(2,sinB)共线,求a,b
,f(C)=0,若向量m=(1,sinA)与向量n=(2,sinB)共线,求a,b
(1)a >0,b>0,若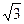 为
为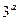 与
与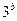 的等比中项,求
的等比中项,求 的最小值
的最小值
(2)已知x>2,求f(x)=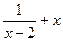 的值域.
的值域.
已知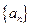 是公差不为零的等差数列,
是公差不为零的等差数列,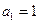 ,且
,且 成等比数列.
成等比数列.
(1)求数列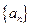 的通项和前n项和
的通项和前n项和 ;
;
(2)令 ,
, 求数列
求数列 的前n项和
的前n项和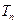
已知|a|=1,|b|=2,
(1)若a∥b,求a·b
(2)若a、b的夹角为60°,求|a+b|;
(3)若a-b与a垂直,求a与b的夹角.