如图,在三棱锥中,底面
,点,分别在棱上,且.
(Ⅰ)求证:平面;
(Ⅱ)当为的中点时,求与平面所成的角的大小;(Ⅲ)是否存在点使得二面角为直二面角?并说明理由.
(本小题满分14分)设函数f (x)满足f (0) =1,且对任意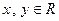 ,都有f (xy+1) = f (x) f (y)-f (y)-x+2.(I)求f (x) 的解析式;(II)若数列{an}满足:an+1=3f (an)-1(nÎ N*),且a1=1,求数列{an}的通项公式;
,都有f (xy+1) = f (x) f (y)-f (y)-x+2.(I)求f (x) 的解析式;(II)若数列{an}满足:an+1=3f (an)-1(nÎ N*),且a1=1,求数列{an}的通项公式;
(Ⅲ)求数列{an}的前n项和Sn.
(本小题满分14分)
(本题14分).如图所示,在正三棱柱ABC-A1B1C1中,
底面边长和侧棱长都是2,D是侧棱CC1上任意一点,E是
A1B1的中点.
(1)求证:A1B1//平面ABD.
(2)求证:
(3)求三棱锥C-ABE的体积.
(本小题满分12分)已知向量 ,
,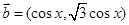 ,函数
,函数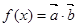 .
.
(1)求函数 的最小正周期和值域;
的最小正周期和值域;
(2)在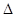
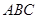 中,
中,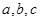 分别是角
分别是角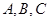 的对边,且
的对边,且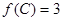 ,
,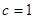 ,
,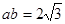 ,且
,且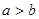 ,求
,求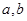
在△ABC中,角A、B、C所对的边分别是a、b、c,则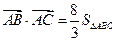 (其中S△ABC为△ABC的面积).
(其中S△ABC为△ABC的面积).
(1)求sin2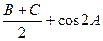 ;
;
(2)若b=2,△ABC的面积S△ABC=3,求a.
(本小题满分12分)如图,已知椭圆C: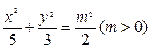 ,经过椭圆C的右焦点F且斜率为k(k≠0)的直线l交椭圆C于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.(1)是否存在k,使对任意m>0,总有
,经过椭圆C的右焦点F且斜率为k(k≠0)的直线l交椭圆C于A、B两点,M为线段AB的中点,设O为椭圆的中心,射线OM交椭圆于N点.(1)是否存在k,使对任意m>0,总有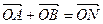 成立?若存在,求出所有k的值;
成立?若存在,求出所有k的值;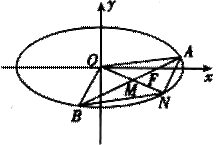 (2)若
(2)若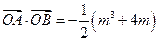 ,求实数k的取值范围.
,求实数k的取值范围.