为了拓展网络市场,腾讯公司为 用户推出了多款
用户推出了多款 应用,如“
应用,如“ 农场”、“
农场”、“ 音乐”、“
音乐”、“ 读书”等.某校研究性学习小组准备举行一次“
读书”等.某校研究性学习小组准备举行一次“ 使用情况”调查,从高二年级的一、二、三、四班中抽取10名学生代表参加,抽取不同班级的学生人数如下表所示:
使用情况”调查,从高二年级的一、二、三、四班中抽取10名学生代表参加,抽取不同班级的学生人数如下表所示:
| 班级 |
一班 |
二班 |
三班 |
四班 |
| 人数 |
2人 |
3人 |
4人 |
1人 |
(I)从这10名学生中随机选出2名,求这2人来自相同班级的概率;
(Ⅱ) 假设在某时段,三名学生代表甲、乙、丙准备分别从 农场、
农场、 音乐、
音乐、 读书中任意选择一项,他们选择
读书中任意选择一项,他们选择 农场的概率都为
农场的概率都为 ;选择
;选择 音乐的概率都为
音乐的概率都为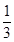 ;选择
;选择 读书的概率都为
读书的概率都为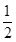 ;他们的选择相互独立.设在该时段这三名学生中选择
;他们的选择相互独立.设在该时段这三名学生中选择 读书的总人数为随机变量
读书的总人数为随机变量 ,求随机变量
,求随机变量 的分布列及数学期望
的分布列及数学期望 .
.
已知向量 ,
, ,
, ,
,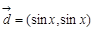 .
.
(1)当 时,求向量
时,求向量 与
与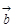 的夹角
的夹角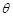 ;
;
(2)当 时,求
时,求 的最大值;
的最大值;
(3)设函数 ,将函数
,将函数 的图像向右平移s个长度单位,向上平移t个长度单位
的图像向右平移s个长度单位,向上平移t个长度单位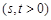 后得到函数
后得到函数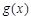 的图像,且
的图像,且 ,令
,令 ,求
,求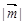 的最小值.
的最小值.
已知向量 ,设函数
,设函数 .
.
(1)求 的单调增区间;
的单调增区间;
(2)若 ,求
,求 的值.
的值.
设集合 ,集合
,集合 ,集合C为不等式
,集合C为不等式 的解集.
的解集.
(1)求 ;
;
(2)若 ,求a的取值范围.
,求a的取值范围.
A,B,C为△ABC的三内角,其对边分别为a, b, c,若 .
.
(1)求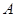 ;
;
(2)若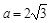 ,
,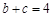 ,求△ABC的面积.
,求△ABC的面积.
(本小题满分14分)
已知椭圆 的两个焦点的坐标分别为
的两个焦点的坐标分别为
 ,
,
 ,并且经过点(
,并且经过点( ,
, ),M、N为椭圆
),M、N为椭圆 上关于
上关于 轴对称的不同两点.
轴对称的不同两点.
(1)求椭圆 的标准方程;
的标准方程;
(2)若 ,试求点
,试求点 的坐标;
的坐标;
(3)若 为
为 轴上两点,且
轴上两点,且 ,试判断直线
,试判断直线 的交点
的交点 是否在椭圆
是否在椭圆 上,并证明你的结论.
上,并证明你的结论.