如图(甲)所示,边长为L=2.5m、质量m=0.50kg的正方形金属线框,平放在光滑的水平桌面上,磁感应强度B=0.80T的匀强磁场方向竖直向上。t=0s时,金属线框的一边ab与磁场的边界MN重合.在变力F作用下金属线框由静止开始向左运动,测得金属线框中的电流随时间变化的图象如图(乙)所示.已知金属线框的总电阻为R=4.0Ω.
(1)试判断金属线框从磁场中拉出的过程中,线框中的感应电流方向;
(2)t=5s时,金属线框的速度v;
(3)已知在5s内力F做功1.92J,那么,金属框从磁场拉出过程线框中产生的焦耳热是多少?
(4)金属线框即将离开磁场时拉力F的大小。
跳伞运动员从350m的高空离开直升机,自由下落一段距离后才打开降落伞,设开伞后以2 m/s2的加速度匀减速下降,到达地面的速度为4 m/s,求他下落的总时间及自由下落的距离.(g取10 m/s2)
如图,质量为m=1.0kg的小滑块(可视为质点)放在质量为M=3.0kg的长木板的右端,木板上表面光滑,木板与地面之间的动摩擦因数为μ=0.2,木板长为L=1.0m。开始时两者都处于静止状态,现对木板施加一个水平向右的恒力F=12N,经过一段时间撤去F。为了使小滑块不掉下木板,试求:水平恒力F作用的最长时间。(g取10m/s2) 。
。
如右图所示,小车在水平路面上加速向右运动,用一条水平绳和一条斜绳(斜绳与竖直方向的夹角θ=30°)把一个质量为m的小球系于车内。不计绳的质量,求下列两种情况下,两绳对小球的拉力大小:
(1)小车以加速度a1=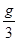 运动;
运动;
(2)小车以加速度a2=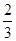 g运动。
g运动。
将质量为0.5kg的小球以14m/s的初速度竖直向上抛出,运动中小球受到的空气阻力大小恒为2.1N。求:
(1)小球上升的加速度大小;
(2)小球能上升的最大高度。
如图所示,物体重为G=100N,与斜面间的动摩擦因数为μ=0.2,用平行于斜面向上的拉力F拉物体,使物体沿斜面匀速向上运动,求拉力F的大小。