下面几种推理是类比推理的是 ( )
A.两条直线平行,同旁内角互补,如果∠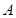 和∠ 和∠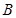 是两条平行直线的同旁内角,则∠ 是两条平行直线的同旁内角,则∠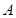 +∠ +∠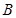 =1800 =1800 |
| B.由平面三角形的性质,推测空间四边形的性质 |
| C.某校高二级有20个班,1班有51位团员,2班有53位团员,3班有52位团员,由此可以推测各班都超过50位团员. |
D.一切偶数都能被2整除,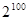 是偶数,所以 是偶数,所以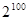 能被2整除. 能被2整除. |
若 均为单位向量,则“
均为单位向量,则“ ”是“
”是“ ”的(
”的( 条件。
条件。
| A.充分非必要 | B.必要非充分 | C.既不充分也不必要 | D.充要 |
定义域是一切实数的函数 ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数 (
( )
)
使得 对任意实数
对任意实数 都成立,则称
都成立,则称 是一个“
是一个“ —伴随函数”. 有
—伴随函数”. 有
下列关于“ —伴随函数”的结论:
—伴随函数”的结论:
① 是常数函数中唯一一个“
是常数函数中唯一一个“ —伴随函数”;
—伴随函数”;
②“ —伴随函数”至少有一个零点;
—伴随函数”至少有一个零点;
③ 是一个“
是一个“ —伴随函数”;
—伴随函数”;
其中正确结论的个数是()
| A.1个; | B.2个; | C.3个; | D.0个; |
已知 是等差数列
是等差数列 的前n项和,且
的前n项和,且 ,有下列四个命
,有下列四个命
题,假命题的是()
A.公差 ; ; |
B.在所有 中, 中, 最大; 最大; |
C.满足 的 的 的个数有11个; 的个数有11个; |
D. ; ; |
已知函数 的图像如左图所示,则函数
的图像如左图所示,则函数 的图像可能是()
的图像可能是()
设 ,则“
,则“ ”是“
”是“ ”的 ( )
”的 ( )
| A.充分而不必要条件; | B.必要而不充分条件; |
| C.充分必要条件; | D.既不充分也不必要条件; |