在平面直角坐标系 中,已知圆
中,已知圆 和圆
和圆 .
.
(1)若直线 过点
过点 ,且被圆
,且被圆 截得的弦长为
截得的弦长为 ,求直线
,求直线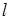 的方程;
的方程;
(2)在平面内是否存在一点 ,使得过点
,使得过点 有无穷多对互相垂直的直线
有无穷多对互相垂直的直线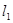 和
和 ,它们分别与圆
,它们分别与圆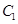 和圆
和圆 相交,且直线
相交,且直线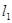 被圆
被圆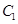 截得的弦长的
截得的弦长的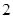 倍与直线
倍与直线 被圆
被圆 截得的弦长相等?若存在,求出所有满足条件的
截得的弦长相等?若存在,求出所有满足条件的 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
((本小题满分12分)
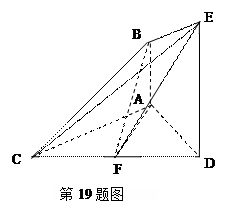
如图,已知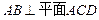 ,
,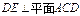 ,
,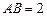 ,
,
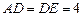 ,
, .
.
(Ⅰ)求证:
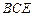 ;
;
(Ⅱ) 若 ,求二面角
,求二面角 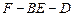 的余弦值.
的余弦值.
(本小题满分12分)
某市为了对学生的数理(数学与物理)学习能力进行分析,从10000名学生中随机抽出100位学生的数理综合学习能力等级分数(6分制)作为样本,分数频数分布如下表:
| 等级得分 |
 |
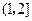 |
 |
 |
 |
 |
| 人数 |
3 |
17 |
30 |
30 |
17 |
3 |
(Ⅰ)如果以能力等级分数大于4分作为良好的标准,从样本中任意抽取2名学生,求恰有1名学生为良好的概率;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值(例如区间 的中点值为1.5)作为代表:
的中点值为1.5)作为代表:
(ⅰ)据此,计算这100名学生数理学习能力等 级分数的期望
级分数的期望 及标准差
及标准差 (精确到0.1);
(精确到0.1);
(ⅱ) 若总体服从正态分布,以样本估计总体,估计该市这10000名学生中数理学习能力等级在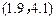 范围内的人数 .
范围内的人数 .
(Ⅲ)从这10000名学生中任意抽取5名同学,
他们数学与物理单科学习能力等级分
数如下表: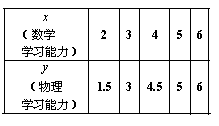
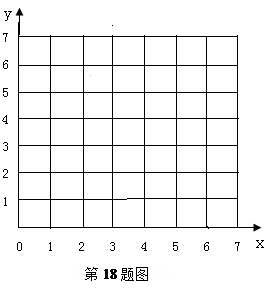
(ⅰ)请画出上表数据的散点图;
(ⅱ)请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程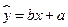 (附参考数据:
(附参考数据: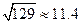 )
)
(本小题满分12分)
已知函数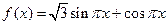 ,
, 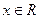 .
.
(Ⅰ)求函数 的最大值和最小值;
的最大值和最小值;
(Ⅱ)设函数 在
在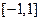 上的图象与
上的图象与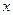 轴的交点从左到右分别为M,N,图象的最高点为P, 求向量
轴的交点从左到右分别为M,N,图象的最高点为P, 求向量 与
与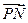 夹角的余弦值.
夹角的余弦值.
(本小题满分12分)
如图,已知在坐标平面xOy内,M、N是x轴上关于原点O对称的两点,P是上半平面内一点,△ PMN的面积为
PMN的面积为 ,点A的坐标为(1+
,点A的坐标为(1+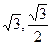 ),
), 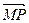 =m·
=m·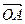 (m为常数),
(m为常数),
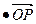


(1)求以M、N为焦点且过点P的椭圆方程;
(2)过点B(-1,0)的直线l交椭圆于C、D两点,交直线x=-4于点E,点B、E分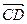 的比分别为λ1、λ2,求λ1+λ2的值。
的比分别为λ1、λ2,求λ1+λ2的值。
本小题满分12分)
某商店搞促销活动,规则如下:木箱内放有5枚白棋子和5枚黑棋子,顾客从中一次性任意取出5枚棋子,如果取出的5枚棋子中恰有5枚白棋子或4枚白棋子或3枚白棋子,则有奖品,奖励办法如下表:
| 取出的棋子 |
奖品 |
| 5枚白棋子 |
价值50元的商品 |
| 4枚白棋子 |
价值30元的商品 |
| 3枚白棋子 |
价值10元的商品 |
如果取出的不是上述三种情况,则顾客需用50元购买商品.
(1)求获得价值50元的商品的概率;
(2)求获得奖品的概率 ;
;
(3)如果顾客所买商品成本价为10元,假设有 10 000人次参加这项促销活动,则商家可以获得的利润大约是多少?(精确到元)
10 000人次参加这项促销活动,则商家可以获得的利润大约是多少?(精确到元)