已知直线l的参数方程为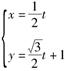 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 为参数).
为参数).
(I )已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4, ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;
(II )设点Q是曲线C上的一个动点,求点Q到直线l的距离的最小值与最大值.
(1)已知角θ的终边上一点P(x,3) (x≠0),且cos θ= x,求sin θ,tan θ.
x,求sin θ,tan θ.
( 2)已知 ,求
,求 的值.
的值.
某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示(在答题卡上).
(Ⅰ)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;
(Ⅱ)为了能选拔出最优秀的学生,该高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官的面试,求第四组至少有一名学生被考官A面试的概率?
设有关于 的一元二次方程
的一元二次方程 .
.
(1)若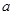 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若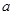 是从区间[0,3]中任取的一个数,
是从区间[0,3]中任取的一个数, 是从区间[0,2]中任取的一个数,求上述方程有实根的概率;
是从区间[0,2]中任取的一个数,求上述方程有实根的概率;
现有8名奥运会志愿者,其中志愿者 通晓日语,
通晓日语, 通晓俄语,
通晓俄语,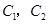 通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
通晓韩语.从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
(Ⅰ)求 被选中的概率;
被选中的概率;
(Ⅱ)求 和
和 不全被选中的概率.
不全被选中的概率.
如图所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中的数学成绩.乙组记录中有一个数据模糊,无法确认,在图中以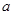 表示.已知甲、乙两个小组的数学成绩的平均分相同.
表示.已知甲、乙两个小组的数学成绩的平均分相同.
(1)求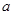 的值;
的值;
(2)求乙组四名同学数学成绩的方差;
(3)分别从甲、乙两组同学中各随机选取一名同学,求这两名同学数学成绩之差的绝对值为3的概率.
(注:方差 ,其中
,其中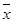 为
为 ,
,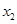 ,…,
,…, 的平均数)
的平均数)