在水平地面上有一点光源S,被不透明的罩遮住,在罩的正上方开一小孔,一束光经过小孔竖直照到距地面高度为3m的水平放置的平面镜上,如图所示,若平面镜突然开始绕水平轴O顺时针转动,在0.1s内转过π/6的角,那么由镜面反射到水平地面上的光斑在这0.1s内沿水平地面移动的平均速度?
登山运动中,小张用100 min(分钟)由宿营地X爬到山顶Y。在山道上通过的路程是2400 m,相对于X升高了1200 m,如下图所示.
(1) 小张由X运动到Y总的位移的大小?
(2) 计算他爬山的平均速度的大小.
(3) 他的朋友小李从Z点爬山,比小张晚20 min开始,平均速率为0. 5 m/s ,还比小张早20 min到达山顶,问小李由Z爬到Y共通过了多少路程?
(8分)一子弹击中木板的速度是600 m / s ,历时0.02 s 穿出木板,穿出木板时的速度为300 m/s ,则子弹穿过木板时的加速度大小和方向?
如左图所示,两根足够长的光滑直金属导轨 、
、 平行放置在倾角为
平行放置在倾角为 的绝缘斜面上,两导轨间距为
的绝缘斜面上,两导轨间距为 。
。 、
、 两点间接有阻值为
两点间接有阻值为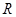 的电阻。一根质量为
的电阻。一根质量为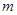 的均匀直金属杆
的均匀直金属杆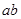 放在两导轨上,并与导轨垂直。整套装置处于磁感应强度为
放在两导轨上,并与导轨垂直。整套装置处于磁感应强度为 的匀强磁场中,磁场方向垂直斜面向下。导轨和金属杆的电阻可忽略。用与导轨平行且向上的恒定拉力
的匀强磁场中,磁场方向垂直斜面向下。导轨和金属杆的电阻可忽略。用与导轨平行且向上的恒定拉力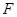 作用在金属杆上,金属杆
作用在金属杆上,金属杆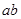 沿导轨向上运动,最终将做匀速运动。当改变拉力
沿导轨向上运动,最终将做匀速运动。当改变拉力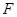 的大小时,相对应的匀速运动速度
的大小时,相对应的匀速运动速度 也会改变,
也会改变, 和
和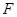 的关系如右图所示。
的关系如右图所示。
(1)金属杆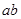 在匀速运动之前做作什么运动?
在匀速运动之前做作什么运动?
(2)若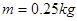 ,
, ,
, ,取重力加速度
,取重力加速度 ,试求磁感应强度
,试求磁感应强度 的大小及
的大小及 角的正弦值
角的正弦值
如下图所示,在xoy直角坐标系中,第Ⅰ象限内分布着方向垂直纸面向里的匀强磁场,第Ⅱ象限内分布着方向沿y轴负方向的匀强电场。初速度为零、带电量为q、质量为m的离子经过电压为U的电场加速后,从x上的A点垂直x轴进入磁场区域,经磁场偏转后过y轴上的P点且垂直y轴进入电场区域,在电场偏转并击中x轴上的C点。已知OA=OC=d。求: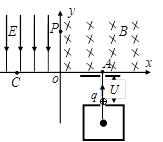
(1)磁感强度B的大小.
(2)电场强度E的大小.
(3)离子从A到C运动的时间.
如图所示,在竖直向上磁感强度为B的匀强磁场中,放置着一个宽度为L的金属框架,框架的右端接有电阻R.一根质量为m,电阻忽略不计的金属棒受到外力冲击后,以速度v沿框架向左运动.已知棒与框架间的摩擦系数为μ,在整个运动过程中,通过电阻R的电量为q,设框架足够长.求: (1)棒运动的最大距离;
(1)棒运动的最大距离;
(2)电阻R上产生的热量。