已知阿伏伽德罗常数为6.0×1023mol-1,在标准状态(压强p0=1atm、温度t0=0℃)下理想气体的摩尔体积都为22.4L,已知第(2)问中理想气体在状态C时的温度为27℃,求该气体的分子数(计算结果保留两位有效数字).
如图所示,一条长为L的绝缘细线上端固定,下端拴一质量为m的带电小球,将它置于水平方向的匀强电场中,电场强度为E,已知当细线与竖直方向的夹角为α时,小球处于平衡位置A点,问在平衡位置给小球多大的速度vA,刚好能使之在电场中作竖直平面内的完整圆周运动?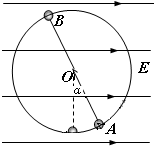
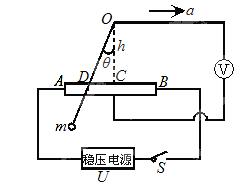
如图所示是一种悬球式加速度仪,它可以用来测定沿水平轨道做匀加速直线运动的列车的加速度。m是一个金属球,它系在细金属丝的下端,金属丝的上端悬挂在O点,AB是一根长为l的电阻丝,其阻值为R。金属丝与电阻丝接触良好,摩擦不计。电阻丝的中点C焊接一根导线.从O点也引出一根导线,两线之间接入一个电压表V(金属丝和导线电阻不计)。图中虚线OC与AB相垂直,且OC=h,电阻丝AB接在电压恒为U的直流稳压电源上。整个装置固定在列车中使AB沿着车前进的方向。列车静止时金属丝呈竖直状态;当列车加速或减速前进时,金属线将偏离竖直方向θ,从电压表的读数变化可以测出加速度的大小。当列车向右做匀加速直线运动时,试写出加速度a与θ角的关系及加速度a与电压表读数U′的对应关系。
这个装置能测得的最大加速度是多少?
如图所示,两带有等量异电荷的平行金属板M、N竖直放置,M、N两板间的距离d=0.5m。现将一质量为m=1×10-2kg、电荷量 的带电小球从两极左斜上方A点以
的带电小球从两极左斜上方A点以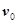 =4m/s的初速度水平抛出,A点距离两板上端的高度h=0.2m,之后小球恰好从靠近M板上端处进入两板间,沿直线运动碰到N板上的B点,不计空气阻力,取g=10m/s2,设匀强电场只存在于M、N之间。求:
=4m/s的初速度水平抛出,A点距离两板上端的高度h=0.2m,之后小球恰好从靠近M板上端处进入两板间,沿直线运动碰到N板上的B点,不计空气阻力,取g=10m/s2,设匀强电场只存在于M、N之间。求:
两极板间的电势差;
小球由A到B所用总时间;
小球到达B点时的动能。
如图所示的电路中,R1=3Ω,R2=9Ω,R3=6Ω,电源电压U=24V保持不变。当开关S1、S2均开启和均闭合时,灯泡L都同样正常发光。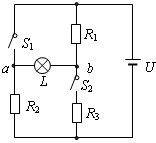
画出两种情况的等效电路图,并标出流经灯泡的电流方向;
求灯泡正常发光时的电阻RL和电压UL。
一电动小车沿如图所示的路径运动,小车从A点由静止出发,沿粗糙的水平直轨道运动L后,由B点进入半径为R的光滑竖直圆形轨道,运动一周后又从B点离开圆轨道进入水平光滑轨道BC段,在C与平面D间是一蓄水池.已知小车质量m=0.lkg、L=l0m、R=0.32m、h=l.25m、s=l.50m,在AB段所受阻力为0.3N.小车只在AB路段可以施加牵引力,牵引力的功率为P=l.5W,其他路段电动机关闭.问:要使小车能够顺利通过圆形轨道的最高点且能落在右侧平台D上,小车电动机至少工作多长时间?(g取l0m/s2)