（本题14分）在平面直角坐标系中，已知抛物线经过
、
、
三点．
⑴ 求抛物线的解析式；
⑵ 若点M为第三象限内抛物线上一动点，点M的横坐标为m,△AMB的面积为S．求S关于m的函数关系式，并求出S的最大值；
⑶ 若点P是抛物线上的动点，点Q是直线
上的动点，判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．
以直线为对称轴，画出下列图形的另一部分使它们成为轴对称图形：
将16个相同的小正方形拼成正方形网格，并将其中的两个小正方
形涂成黑色，请你用两种不同的方法分别在图甲、图乙中再将两个空白的小正方形
涂黑，使它成为轴对称图形
一名潜水员在水下方80米处发现一条鲨鱼在离他不远处的上方25米的位置往下游追逐猎物，当它向下游42米后追上猎物，此时猎物垂死挣扎，立刻反向上游，鲨鱼紧紧尾随，又游了10米后被鲨鱼一口吞吃.求鲨鱼吃掉猎物时所在的位置；
与刚开始潜水员发现鲨鱼的位置相比，鲨鱼的位置有什么变化？
观察数轴
-5 –4 –3 –2 –1 0 1 2 3 4 5
可得：到点-2和点2距离相等的点表示的数是0，有这样的关系0=
（-2+2）；
根据上面的结论，解答下面的问题．到点100和到点999距离相等的点表示的数是多少？
到点
距离相等的点表示的数是多少？到点m和点–n距离相等的点表示的数是多少？
先观察下图的立体图形，再分别画出从它的正面、左面、上面三个方向所看到的平面图形.
如图，在正方形ABCD中，E是CD边上的中点，AC与BE相交于点F，连接DF.(注：正方形的四边相等，四个角都是直角，每一条对角线平分一组对角).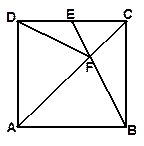
(1) 在不增加点和线的前提下,直接写出图中所有的全等三角形;
连接AE,试判断AE与DF的位置关系,并证明你的结论;
延长DF交BC于点M,试判断BM与MC的数量关系，并说明理由。