某商场将每件进价为80元的某种商品原来按每件100元出售，一天可售出100件，后来经过市场调查，发现这种商品每降低1元，其销量可增加10件。
⑴求商场经营该商品原来一天可获利润多少元？
⑵设后来该商品每件降价x元，商场一天可获利y元。
①若商场经营该商品一天要获利润2160元，则每件商品应降价多少元？
②求出y与x之间的函数关系式，并通过画该函数图像的草图，观察其图象的变化趋势，结合题意写出该x取何值时，商场所获利润不少于2160元？
先化简再求值（本题6分）
，其中a满足
解不等式组
已知四边形ABCD，点E是射线BC上的一个动点（点E不与B、C两点重合），线段BE的垂直平分线交射线AC于点P，联结DP，PE.
（1）若四边形ABCD是正方形，猜想PD与PE的关系，并证明你的结论.
（2）若四边形ABCD是矩形，（1）中的PD与PE的关系还成立吗？（填：成立或不成立）.
（3）若四边形ABCD是矩形，AB=6，cos∠ACD=
，设AP=x，△PCE的面积为y,当AP>
AC时，求y与x之间的函数关系式.
已知：如图，二次函数y=a(x+1)2－4的图象与x轴分别交于A、B两点，与y轴交于点D，点C是二次函数y=a(x+1)2－4的图象的顶点，CD=
.
（1）求a的值.
（2）点M在二次函数y=a(x+1)2－4图象的对称轴上，
且∠AMC=∠BDO，求点M的坐标．
（3）将二次函数y=a(x+1)2－4的图象向下平移k（k＞0）个单位，平移后的图象与直线CD分别交于E、F两点（点F在点E左侧），设平移后的二次函数的图象的顶点为C1，与y轴的交点为D1，是否存在实数k，使得CF⊥FC1，若存在，求出k的值；若不存在，请说明理由．
已知二次函数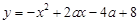
（1）求证：无论a为任何实数，二次函数的图象与x轴
总有两个交点.
（2）当x≥2时，函数值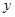
随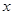
的增大而减小，求
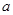的取
值范围.
（3）以二次函数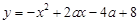图象的顶点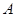
为一个顶点作该二次函数图象的内接正三角形
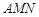（M，N两点在二次函数的图象上），请问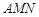：△的面积是与a无关的定值吗？若是，请求出这个定值；若不是，请说明理由.