如图所示，两根电阻不计的足够长光滑平行金属导轨与水平面夹角为
，导轨间距为l，所在平面的正方形区域abcd内存在有界匀强磁场，磁感应强度大小为B，方向垂直于斜面向上。如图所示，将甲、乙两阻值相同，质量均为m的相同金属杆放置在导轨上，甲金属杆处在磁场的上边界，甲、乙相距l。从静止释放两金属杆的同时，在金属杆甲上施加一个沿着导轨的外力F，使甲金属杆在运动过程中始终沿导轨向下做匀加速直线运动，且加速度大小a=gsinθ，乙金属杆进入磁场即做匀速运动。
（1）求每根金属杆的电阻R；
（2）从释放金属杆开始计时，写出从计时开始到甲金属杆离开磁场的过程中外力F随时间t变化的关系式，并说明F的方向；
（3）若从开始释放两杆到乙金属杆离开磁场，乙金属杆共产生热量Q，试求此过程中外力F对甲做的功。
如图所示，一束电子（电量为e）以速度v0垂直射入磁感应强度为B，宽为d的匀强磁场中，穿出磁场时速度方向与电子原来入射方向的夹角为30°，则电子的质量是多少？穿过磁场的时间是多少？
行时间质谱仪主要由脉冲阀、激光器、加速电场、偏转电场和探测器组成，可以对气体分子进行分析。如图所示,脉冲阀P喷出微量气体，经激光照射产生不同价位的离子，自a板小孔进入a、b间的加速电场，从b板小孔射出，沿中线方向进入M、N板间的偏转控制区，到达探测器。已知加速电场a、b板间距为d，偏转电场极板M、N的长度为L1，宽度为L2。不计离子重力及进入a板时的初速度。
（1）设离子比荷为k（k=q/m），若a、b间的加速电压为U1，试求离子进入偏转电场时的初速度v0；
（2）当a、b间的电压为U1时，在M、N间加上适当的电压U2，离子从脉冲阀P喷出到到达探测器的全部飞行时间为t。请推导出离子k比荷的表达式；
（3）在某次测量中探测器始终无法观察到离子，分析原因是离子偏转量过大，打到极板上，请说明如何调节才能观察到离子（无需论证）？
如图所示在A上的放射源C，可向各个方向射出速率为v的电子流，B为金属网，A、B连接在电路上，电源电动势为E，内阻为r，滑动变阻器的总阻值为R。图中滑动变阻器滑片置于中点，AB间的间距为d，M为足够大的荧光屏，M紧挨着金属网外侧。已知电子质量为m，电量为e。不计电子所形成的电流对电路的影响，求：
（1）闭合开关S后，AB间场强的大小是多少？
（2）电子到达金属网B的最长时间是多少?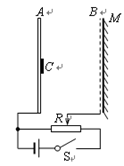
如图所示，真空中存在空间范围足够大的、方向水平向右的匀强电场，在电场中，一个质量为m、带电量为q的粒子从O点出发，初速度的大小为v0，在重力和电场力的共同作用下恰能沿与场强的反方向成θ角做匀减速直线运动，求：
（1）匀强电场的场强的大小；
（2）粒子运动的最高点与出发点之间的电势差。
为了缩短下楼的时间，消防员往往抱着楼房外的竖直杆直接滑下，设消防员先以可能的最大加速度沿杆做匀加速直线运动，再以可能的最大加速度沿杆做匀减速直线运动．一名质量m=65kg的消防员，在沿竖直杆无初速度滑至地面的过程中，重心共下降了h=11.4m，该消防员与杆之间的滑动摩擦力最大可达到fm=975N，消防员着地的速度不能超过v=6m/s．（g=10m/s2）求：
（1）消防员下滑过程中速度的最大值；
（2）消防员下滑过程的最短时间．