“五·一”期间,九年一班同学从学校出发,去距学校6千米的公园游玩,同学们分为步行和骑自行车两组,在去公园的全过程中,骑自行车的同学比步行的同学少用40分钟,已知骑自行车的速度是步行速度的3倍.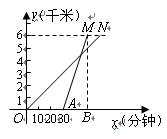
(1)求步行同学每小时走多少千米?
(2)图是两组同学前往公园时的路程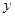 (千米)与时间
(千米)与时间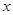 (分钟)的函数图象.
(分钟)的函数图象.
完成下列填空:
①表示骑车同学的函数图象是线段 ;
②已知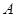 点坐标
点坐标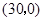 ,则
,则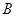 点的坐标为( ).
点的坐标为( ).
如图,已知左右并排的两棵树高分别是AB=8m,CD=12m,两树的根部的距离BD=5m,小明眼睛离地面的高度EF为1.6m,他沿着正对这两棵树的一条水平直路从左到右前进,当他与左边较低的树的距离小于多少时,就不能看到右边较高的树的顶端点C? 
如图,在矩形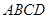 中,对角线
中,对角线 与
与 相交于点
相交于点 ,过点
,过点 作
作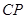 ∥
∥ ,
,
过点 作
作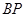 ∥
∥ ,两线相交于点
,两线相交于点 。
。
求证:四边形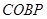 是菱形.
是菱形.
已知,如图,AB和DE是直立在地面上的两根立柱AB=6m,某一时刻AB在太阳光下的投影BC=3m。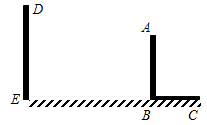
(1)请你在图中画出此时DE在太阳光下的投影EF;
(2)在测量AB的投影时,同时测量出DE在太阳光下的投影EF长为6m,请你计算DE的长。
在四个完全相同的小球上分别写上1,2,3,4四个数字,然后装入一个不透明的口袋内搅匀. 从口袋内任取出一个球记下数字后作为点P的横坐标x,放回袋中搅匀,然后再从袋中取出一个球记下数字后作为点P的纵坐标y,请你用画树状图或列表的方法表示所有等可能的结果,并求点P(x,y)落在直线y=x上的概率是多少?
如图,在平面直角坐标系中,已知△ABC的三个顶点A、B、C都在格点上,坐标分别为(4,2),(1,1),(2,-2)。
(1)将△ABC三个顶点的横坐标、纵坐标都分别乘-2,写出变化后的三个顶点A1、B1、C1的坐标。
(2)画出以A1、B1、C1为顶点的△A1B1C1。
(3)△ABC与△A1B1C1是位似图形吗?如果是位似图形,请指出位似中心和位似比。如果不是,请说明理由。