开学初，小芳和小亮去学校商店购买学习用品，小芳用18元钱买了1枝钢笔和3本笔记本；小亮用31元买了同样的钢笔2枝和笔记本5本。
（1）求每枝钢笔和每本笔记本的价格；
（2）校运会后，班主任拿出200元学校奖励基金交给班长，购买上述价格的钢笔和笔记本共48件作为奖品，奖给校运会中表现突出的同学，要求笔记本数不少于钢笔数，共有多少种购买方案？请你一一写出。
如图，从热气球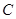
上测得两建筑物
、
底部的俯角分别为30°和
．如果这时气球的高度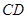
为90米．且点、
、在同一直线上，求建筑物、间的距离．
如图，AC是菱形ABCD的对角线，点E、F分别在边AB、AD上，且AE="AF." 求证：CE=CF
解不等式组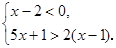
并将解集在数轴上表示.
计算：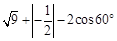
如图1，已知直线y=kx与抛物线
交于点A（3，6）．
（1）求直线y=kx的解析式和线段OA的长度；
（2）点P为抛物线第一象限内的动点，过点P作直线PM，交x轴于点M（点M、O不重合），交直线OA于点Q，再过点Q作直线PM的垂线，交y轴于点N．试探究：线段QM与线段QN的长度之比是否为定值？如果是，求出这个定值；如果不是，说明理由；
（3）如图2，若点B为抛物线上对称轴右侧的点，点E在线段OA上（与点O、A不重合），点D（m，0）是x轴正半轴上的动点，且满足∠BAE=∠BED=∠AOD．继续探究：m在什么范围时，符合条件的E点的个数分别是1个、2个？