设函数
 (提示 :
(提示 :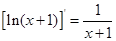 )
)
(1)若函数 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数 的取值范围;
的取值范围;
(2) 若 ,证明对任意的正整数n,不等式
,证明对任意的正整数n,不等式 都成立.
都成立.
在 中,角A,B,C的对边分别为a,b,c,若
中,角A,B,C的对边分别为a,b,c,若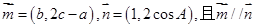 .
.
(1)求B;
(2)设函数 ,求函数
,求函数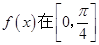 上的取值范围.
上的取值范围.
已知函数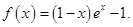
(1)求函数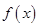 的最大值;
的最大值;
(2)若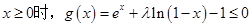 ,求
,求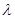 的取值范围.
的取值范围.
(3)证明: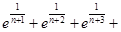 +
+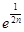
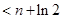 (n
(n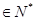 )
)
已知中心在原点,对称轴为坐标轴的椭圆C的一个焦点在抛物线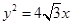 的准线上,且椭圆C过点
的准线上,且椭圆C过点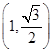 .
.
(1)求椭圆C的方程;
(2)点A为椭圆C的右顶点,过点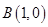 作直线
作直线 与椭圆C相交于E,F两点,直线AE,AF与直线
与椭圆C相交于E,F两点,直线AE,AF与直线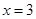 分别交于不同的两点M,N,求
分别交于不同的两点M,N,求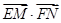 的取值范围.
的取值范围.
某市为控制大气PM2.5的浓度,环境部门规定:该市每年的大气主要污染物排放总量不能超过55万吨,否则将采取紧急限排措施.已知该市2013年的大气主要污染物排放总量为40万吨,通过技术改造和倡导绿色低碳生活等措施,此后每年的原大气主要污染物排放最比上一年的排放总量减少10%.同时,因为经济发展和人口增加等因素,每年又新增加大气主要污染物排放量 万吨.
万吨.
(1)从2014年起,该市每年大气主要污染物排放总量(万吨)依次构成数列 ,求相邻两年主要污染物排放总量的关系式;
,求相邻两年主要污染物排放总量的关系式;
(2)证明:数列 是等比数列;
是等比数列;
(3)若该市始终不需要采取紧急限排措施,求m的取值范围.
如图,在四棱锥P-ABCD中,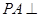 平面ABCD,AD//BC,
平面ABCD,AD//BC,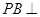 AC,
AC,
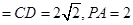 ,点M在线段PD上.
,点M在线段PD上.
(1)求证: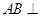 平面PAC;
平面PAC;
(2)若二面角M-AC-D的大小为 ,试确定点M的位置.
,试确定点M的位置.