已知：抛物线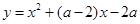
（
为常数，且
）.
（1）求证：抛物线与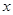
轴有两个交点；
（2）设抛物线与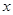轴的两个交点分别为
、
（
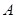在左侧），与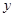
轴的交点为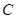
.
当
时，求抛物线的解析式；
如图，CD是经过∠BCA顶点C的一条直线，CA=CB，E、F分别是直线CD上两点，且∠BEC=∠CFA=∠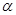
．
（1）若直线CD经过∠BCA的内部，且E、F在射线CD上，请解决下面两个问题：
①如图1，若∠BCA=90°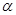，∠=90°，则BE CF；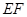
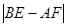（填“＞”、“＜”或“=”）；
②如图2，若0°＜∠BCA＜180°，请添加一个关于∠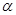与∠BCA关系的条件 ，使①中的两个结论仍然成立，并证明这两个结论．
（2）如图3，若直线CD经过∠BCA的外部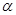，∠=∠BCA，请提出EF、BE、AF三条线段数量关系的合理猜想（不要求证明）．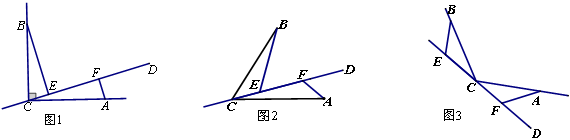
已知AB=AC，AD=AE，∠BAC=∠DAE，直线BD、CE交于点G，
（1）如图1，点D在AC上，求证：∠BGC=∠BAC；
（2）如图2，当点D不在AC上，（1）中的结论还成立吗？若成立，请证明；若不成立，请说明理由．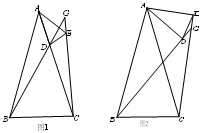
如图，把一个直角△ABC（∠ACB=90°，∠ABC=60°）绕着顶点B顺时针旋转60°，使得点C旋转到AB边上的一点D，点A旋转到点E的位置，F、G分别是BD、BE上的点，且BF=BG，延长CF与DG交于点H，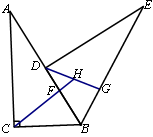
（1）求证：CF=DG；
（2）求∠FHG的度数．
在直角坐标系中，△ABC的三个顶点的位置如图所示，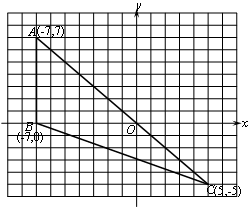
（1）请画出△ABC关于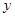
轴对称的
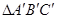（其中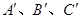
分别是A、B、C的对应点，不写画法）；
（2）直接写出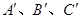三点的坐标：
；
（3）已知BC=13，直接写出BC边上的高．
如图，在△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠BAC=50°，∠C=70°．求∠DAC和∠BOA的度数．