如图，抛物线y＝a(x＋1)(x－5)与x轴的交点为M、N．直线y＝kx＋b
与x轴交于P(－2，0)，与y轴交于C．若A、B两点在直线y＝kx＋b上，且AO=BO=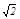
，AO⊥BO．D为线段MN的中点，OH为Rt△OPC斜边上的高．
(1)OH的长度等于___________；k＝___________，b＝____________；
(2)是否存在实数a，使得抛物线y＝a(x＋1)(x－5)上有一点E，满足以D、N、E为顶
点的三角形与△AOB相似?若不存在，说明理由；若存在，求所有符合条件的抛物线的解析式，同时探索所求得的抛物线上是否还有符合条件的E点(简要说明理由)；并进一步探索对符合条件的每一个E点，直线NE与直线AB的交点G是否总满足PB·PG＜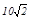
，写出探索过程．
如图，AB是⊙O的直径，C是BA延长线上一点，CD切⊙O于点D，弦DE∥CB，Q是AB上动点，CA＝1，CD是⊙O半径的
倍求⊙O的半径R.
当点Q从点A向点B运动的过程中，图中阴影部分的面积是否发生变化，若发生变化，请你说明理由；若不发生变化，请你求出阴影部分的面积.
已知二次函数y =" -" x2 - x + 在给定的直角坐标系中，画出这个函数的图象；
根据图象，写出当y ＜ 0时，x的取值范围
若将此图象沿x轴向右平移3个单位，请写出平移后图象所对应的函数关系式
在毕业晚会上，同学们表演哪一类型的节目由自己摸球来决定.在一个不透明的口袋中，装有除标号外其它完全相同的A、B、C三个小球，表演节目前，先从袋中摸球一次（摸球后又放回袋中），如果摸到的是A球，则表演唱歌；如果摸到的是B球，则表演跳舞；如果摸到的是C球，则表演朗诵.若小明要表演两个节目，则他表演的节目不是同一类型的概率是多少？
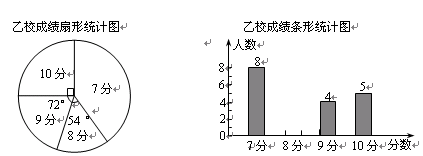
甲、乙两校参加区教育局举办的学生英语口语竞赛，两校参赛人数相等．比赛结束后，发现学生成绩分别为7分、8分、9分、10分（满分为10分）．依据统计数据绘制了如下尚不完整的统计图表．
|
先化简，再求值：
（1+
）·
其中x为数据-1，2，0，2，3的众数