如图，抛物线y＝a(x＋1)(x－5)与x轴的交点为M、N．直线y＝kx＋b
与x轴交于P(－2，0)，与y轴交于C．若A、B两点在直线y＝kx＋b上，且AO=BO=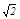
，AO⊥BO．D为线段MN的中点，OH为Rt△OPC斜边上的高．
(1)OH的长度等于___________；k＝___________，b＝____________；
(2)是否存在实数a，使得抛物线y＝a(x＋1)(x－5)上有一点E，满足以D、N、E为顶
点的三角形与△AOB相似?若不存在，说明理由；若存在，求所有符合条件的抛物线的解析式，同时探索所求得的抛物线上是否还有符合条件的E点(简要说明理由)；并进一步探索对符合条件的每一个E点，直线NE与直线AB的交点G是否总满足PB·PG＜
，写出探索过程．
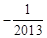的倒数为【】
A． |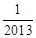
B． |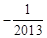
C． |
D． |
我们知道，一元二次方程x2=﹣1没有实数根，即不存在一个实数的平方等于﹣1．若我们规定一个新数“i”，使其满足i2=﹣1（即方程x2=﹣1有一个根为i）．并且进一步规定：一切实数可以与新数进行四则运算，且原有运算律和运算法则仍然成立，于是有i1=i，i2=﹣1，i3=i2•i=（﹣1）•i=﹣i，i4=（i2）2=（﹣1）2=1，从而对于任意正整数n，我们可以得到i4n+1=i4n•i=（i4）n•i=i，同理可得i4n+2=﹣1，i4n+3=﹣i，i4n=1．那么i+i2+i3+i4+…+i2012+i2013的值为【】
| A．0 | B．1 | C．﹣1 | D．i |
下列说法正确的是
| A．一组数据2，5，3，1，4，3的中位数是3 |
| B．五边形的外角和是540度 |
| C．“菱形的对角线互相垂直”的逆命题是真命题 |
| D．三角形的外心是这个三角形三条角平分线的交点 |
）已知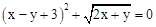
，则x+y的值为【】
| A．0 | B．﹣1 | C．1 | D．5 |
实数a，b，c在数轴上对应的点如图所示，则下列式子中正确的是【】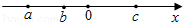
| A．a﹣c＞b﹣c | B．a+c＜b+c | C．ac＞bc | D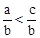． |