(本题12分)如图，一抛物线的顶点A为(2，

(本题12分)如图，一抛物线的顶点A为(2，－1)，交x轴于B、C(B左C右)两点，交y轴于点D，且B(1，0)，坐标原点为O，
(1)求抛物线解析式．
(2)连接CＤ、BD，在x轴上确定点E，使以A、C、E为顶点的三角形与△CBD相似，并求出点E的坐标．
(3)若点M(m，1)是抛物线上对称轴右侧的一点，点Q也在抛物线上，点P在x轴上，是否存在以O、M、P、Q为顶点的四边形是平行四边形，若存在，请直接写出点P的坐标；若不存在，请说明理由．

科目数学题型选择题难度未知

$- 2$ 的倒数是 $($ 　　 $)$

A． $- \frac{1}{2}$ B． $\frac{1}{2}$ C．2D． $- 2$

二次函数 $y = a x^{2} + bx + c (a \neq 0)$ 的大致图象如图所示，顶点坐标为 $(- 2, - 9 a)$ ，下列结论：① $4 a + 2 b + c > 0$ ；② $5 a - b + c = 0$ ；③若方程 $a (x + 5) (x - 1) = - 1$ 有两个根 $x_{1}$ 和 $x_{2}$ ，且 $x_{1} < x_{2}$ ，则 $- 5 < x_{1} < x_{2} < 1$ ；④若方程 $| a x^{2} + bx + c | = 1$ 有四个根，则这四个根的和为 $- 4$ ．其中正确的结论有 $($ 　　 $)$

A．1个B．2个C．3个D．4个

如图，等腰 $Rt Δ ABC$ 中，斜边 $AB$ 的长为2， $O$ 为 $AB$ 的中点， $P$ 为 $AC$ 边上的动点， $OQ ⊥ OP$ 交 $BC$ 于点 $Q$ ， $M$ 为 $PQ$ 的中点，当点 $P$ 从点 $A$ 运动到点 $C$ 时，点 $M$ 所经过的路线长为 $($ 　　 $)$

A． $\frac{\sqrt{2}}{4} π$ B． $\frac{\sqrt{2}}{2} π$ C．1D．2

某几何体由若干个大小相同的小正方体组成，其主视图与左视图如图所示，则组成这个几何体的小正方体最少有 $($ 　　 $)$

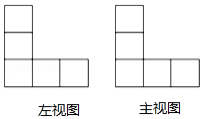
A．4个B．5个C．6个D．7个

如图，在平面直角坐标系 $xOy$ 中， $A (4, 0)$ ， $B (0, 3)$ ， $C (4, 3)$ ， $I$ 是 $ΔABC$ 的内心，将 $ΔABC$ 绕原点逆时针旋转 $90 °$ 后， $I$ 的对应点 $I^{'}$ 的坐标为 $($ 　　 $)$

A． $(- 2, 3)$ B． $(- 3, 2)$ C． $(3, - 2)$ D． $(2, - 3)$

试卷网试题网古诗词网作文网范文网