某学校课题组为了研究学生的数学成绩和物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩,列出如下所示2×2列联表:
| 数学成绩 物理成绩 |
优秀 |
不优秀 |
合计 |
| 优秀 |
5 |
2 |
7 |
| 不优秀 |
1 |
12 |
13 |
| 合计 |
6 |
14 |
20 |
(1)根据题中表格的数据计算,你有多少的把握认为学生的数学成绩与物理成绩之间有关系?
(2)若按下面的方法从这20人(序号1,2,3,…,20)中抽取1人来了解有关情况:将一个标有数字1,2,3,4,5,6的正六面体骰子连续投掷两次,记朝上的两个数字的乘积为被抽取人的序号.试求:①抽到12号的概率;②抽到 “无效序号(序号大于20)”的概率.
参考公式: ,其中
,其中 )
)
临界值表供参考:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
甲盒有标号分别为1、2、3的3个红球;乙盒有标号分别为1、2、…、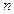
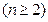
的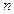 个黑球,从甲、乙两盒中各抽取一个小球,抽到标号为1号红球和
个黑球,从甲、乙两盒中各抽取一个小球,抽到标号为1号红球和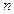 号黑球的概率为
号黑球的概率为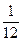 .
.
(Ⅰ)求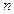 的值;
的值;
(Ⅱ)现从甲乙两盒各随机抽取1个小球,抽得红球的得分为其标号数;抽得黑球,若标号数为奇数,则得分为1,若标号数为偶数,则得分为0,设被抽取的2个小球得分之和为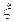 ,求
,求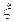 的数学期望
的数学期望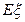 .
.
在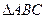 中,角
中,角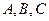 所对的边分别为
所对的边分别为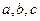 .向量
.向量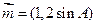 ,
,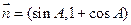 .已知
.已知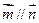 ,
,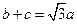 .
.
(Ⅰ)求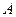 的大小;
的大小;
(Ⅱ)判断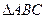 的形状并证明.
的形状并证明.
已知函数 的图象经过点
的图象经过点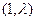 ,且对任意
,且对任意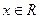 ,都有
,都有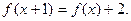 数列
数列 满足
满足
(Ⅰ)当 为正整数时,求
为正整数时,求 的表达式
的表达式
(Ⅱ)设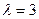 ,求
,求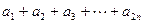
(Ⅲ)若对任意 ,总有
,总有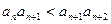 ,求实数
,求实数 的取值范围
的取值范围
已知椭圆C的中心在原点,焦点在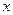 轴上,长轴长是短轴长的
轴上,长轴长是短轴长的 倍且经过点M
倍且经过点M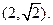
(Ⅰ)求椭圆C的方程
(Ⅱ)过圆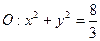 上的任一点作圆的一条切线交
上的任一点作圆的一条切线交 椭圆C与A、B两点
椭圆C与A、B两点
①求证: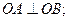
②求|AB|的取值范围
.已知函数 ,
, 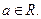
(1)若函数 在
在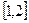 上是减函数,求实数
上是减函数,求实数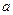 的取值范围
的取值范围
(2)令 ,是否存在实数
,是否存在实数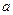 ,当
,当
 (
( 是自然常数)时,函数
是自然常数)时,函数 的最小值是3,若存在,求出
的最小值是3,若存在,求出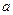 的值;若不存在,说明理由
的值;若不存在,说明理由
(3)当
 时,证明:
时,证明: 