已知A1，A2，B是椭圆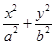
＝1（a>b>0）的顶点（如图），直线l与椭圆交于异于顶点的P，Q两点，且l∥A2B，若椭圆的离心率是
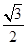，且｜A2B｜＝
。
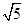（1）求此椭圆的方程；
（2）设直线A1P和直线BQ的倾斜角分别为α，β，试判断α＋β是否为定值？若是，求出此定值；若不是，说明理由。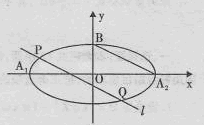
某装置由两套系统M,N组成，只要有一套系统工作正常，该
装置就可以正常工作。每套系统都由三种电子模块T1,T2,T3组成（如图所示已知T1,T2,T3正常工作的概率都是
，且T1,T2,T3能否正常工作相互独立.(注：对每一套系统或每一种电子模块而言,只要有电流通过就能正常工作.)
(I )分别求系统M,N正常工作的概率
；
(II)设该装I中两套系统正常工作的套数为
，求
的分布列和期望.
已知
中，
，
，设
.
(1 )用
表示
；
(11)求
的单调递增区间.
已知奇函数，
的
图象在x=2处的切线方程为
(I )求
的解析式；
(II)是否存
在实数,m,n使得函数
在区间
上的最小值为m，最大值为n.若存在，求出这样一组实数m,n,若不存在，则说明理由.
已知线段AB的两个端点A、B分别在轴、y轴上滑动，
，点M满足
.
(I )求动点M的轨迹E的方程；
(II)若曲线E的所有弦都不能被直线
垂直平分,求实数k的取值范围.
设
是公比大于1的等比数列，
为数列
的前n项和，已知
，且
成等差数列.
(I )求数列
的通项公式
；
(II)若
，求和：