如图所示,用内壁光滑的薄壁细管弯成的“S”形轨道固定于竖直平面内,弯曲部分是由两个半径均为R =" 0.2" m 的半圆平滑对接而成(圆的半径远大于细管内径).轨道底端A与水平地面相切,顶端与一个长为l =" 0.9" m的水平轨道相切B点.一倾角为θ = 37°的倾斜轨道固定于右侧地面上,其顶点D与水平轨道的高度差为h =" 0.45" m,并与其它两个轨道处于同一竖直平面内.一质量为m =" 0.1" kg 的小物体(可视为质点)在A点被弹射入“S”形轨道内,沿轨道ABC运动,并恰好从D点以平行斜面的速度进入斜轨道.小物体与BC段间的动摩擦因数μ = 0.5. (不计空气阻力,g取10 m/s2.sin37°= 0.6,cos37°=" 0.8)" 
(1)小物体从B点运动到D点所用的时间;
(2)小物体运动到B点时对“S”形轨道的作用力大小和方向;
(3)小物体在A点的动能.
如图所示,一个人用一根长1 m,只能承受46 N拉力的绳子,拴着一个质量为1 kg的小球,在竖直平面内做圆周运动.已知圆心O离地面h="6" m,转动中小球在最低点时绳子断了.求: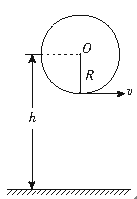
(1)绳子断时小球运动的角速度多大?
(2)绳断后,小球落地点与抛出点间的水平距离
AB是竖直平面内的四分之一光滑圆弧轨道,在下端B与水平直轨平滑相切,如图10所示。一小木块自A点起由静止开始沿轨道下滑,最后停在C点。已知圆轨道半径为R,小木块的质量为m,小木块运动到B点时的速度为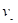 ,水平直轨道的动摩擦因数为
,水平直轨道的动摩擦因数为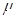 。(小木块可视为质点)求:
。(小木块可视为质点)求:
(1)小木块经过圆弧轨道的B点和水平轨道的C点时,所受轨道支持力NB、NC各是多大?
(2)B、C两点之间的距离x是多大?
交管部门强行推出了“电子眼”,机动车违规现象大幅度减少.现有甲、乙两汽车正沿同一平直马路同向匀速行驶,甲车在前,乙车在后,行驶速度v0均为54km/h.当两车快要到十字路口时,甲车司机看到红灯亮起,于是紧急刹车,乙车司机看到甲车刹车后也紧急刹车(乙车司机的反应时间 =0.4s,反应时间内视为匀速运动).已知甲车、乙车紧急刹车时产生的加速度大小分别为
=0.4s,反应时间内视为匀速运动).已知甲车、乙车紧急刹车时产生的加速度大小分别为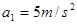 、
、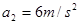 .
.
(1)若甲司机看到红灯时车头距警戒线 ,要避免闯红灯,他的反应时间
,要避免闯红灯,他的反应时间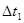 不能超过多少?
不能超过多少?
(2)乙车刹车后经多长时间速度与甲车相等?
(3)为保证两车在紧急刹车过程中不相撞,甲、乙两车刹车前的距离x0至少多大?
一个静止的质量为M的放射性原子核发生衰变,放出一个质量为m、速度大小为v的α粒子,设衰变过程中释放的核能全部转化为新原子核和α粒子的动能,真空中光速为c.求:
① 衰变后新原子核速度大小为多少?
② 衰变过程中质量亏损为多少?
某同学利用DIS实验系统研究一定量理想气体的状态变化,实验后计算机屏幕显示如图所示的P-t图像.已知在状态B时气体的体积为VB=3L,问:
① 气体由A→B,B→C各作什么变化?
② 气体在状态C的体积是多少?