如图甲所示是一打桩机的简易模型。质量m=1kg的物体在拉力F作用下从与钉子接触处由静止开始运动,上升一段高度后撤去F,到最高点后自由下落,撞击钉子,将钉子打入一定深度。物体上升过程中,机械能E与上升高度h的关系图象如图乙所示。不计所有摩擦,g取10m/s2。求: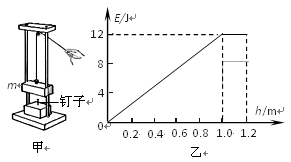
⑴物体上升到1m高度处的速度;
⑵物体上升1 m后再经多长时间才撞击钉子(结果可保留根号);
⑶物体上升到0.25m高度处拉力F的瞬时功率。
边长为L=0.2m的正方形区域内有垂直纸面向里的匀强磁场,穿过该区域磁场的磁感应强度随时间变化的图象如图乙所示,将边长为 ,匝数n=100,线圈电阻r=1.0Ω的正方形线圈abcd放入磁场,线圈所在平面与磁感线垂直,如图甲所示.求:
,匝数n=100,线圈电阻r=1.0Ω的正方形线圈abcd放入磁场,线圈所在平面与磁感线垂直,如图甲所示.求: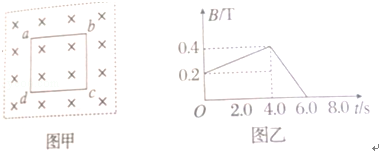
(1)回路中感应电流的方向及磁感应强度的变化率 ;
;
(2)在0~4.0s内通过线圈的电荷量q;
(3)0~6.0s内整个闭合电路中产生的热量.
如图所示,在半径为R=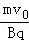 的圆形区域内有垂直纸面向里的匀强磁场,磁感应强度B,圆形区域右侧有一竖直感光板,从圆弧顶点P以速率v0的带正电粒子平行于纸面进入磁场,已知粒子的质量为m,电量为q,粒子重力不计.
的圆形区域内有垂直纸面向里的匀强磁场,磁感应强度B,圆形区域右侧有一竖直感光板,从圆弧顶点P以速率v0的带正电粒子平行于纸面进入磁场,已知粒子的质量为m,电量为q,粒子重力不计.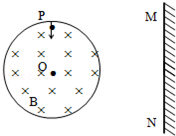
(1)若粒子对准圆心射入,求它在磁场中运动的时间;
(2)若粒子对准圆心射入,且速率为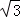 v0,求它打到感光板上时速度的垂直分量;
v0,求它打到感光板上时速度的垂直分量;
(3)若粒子以速度v0从P点以任意角入射,试证明它离开磁场后均垂直打在感光板上.
回旋加速器是用于加速带电粒子流,使之获得很大动能的仪器,其核心部分是两个D形金属扁盒,两盒分别和一高频交流电源两极相接,以便在盒间狭缝中形成匀强电场,使粒子每穿过狭缝都得到加速;两盒放在匀强磁场中,磁场方向垂直于盒底面.离子源置于盒的圆心,释放出电量为q、质量为m的离子,离子最大回旋半径为Rm,磁场强度为B,其运动轨迹如图所示.求:
(1)离子离开加速器时速度多大?
(2)设离子初速度为零,两D形盒间电场的电势差为U,盒间距离为d,求加速到上述能量所需时间(粒子在缝中时间不忽略).
一辆值勤的警车停在公路边,当警员发现从他旁边以10m/s的速度匀速行驶的货车严重超载时,决定前去追赶,经过5.5s后警车发动起来,并以2.5m/s2的加速度做匀加速运动,但警车的行驶速度必须控制在90km/h以内.问:
(1)警车在追赶货车的过程中,两车间的最大距离是多少?
(2)警车发动后要多长时间才能追上货车?
雨后,屋檐还在不断滴着水滴,如图所示.小红认真观察后发现,这些水滴都是在质量积累到足够大时才由静止开始下落.她测得,屋檐到施窗台的距离H=3.2m,窗户的高度为h=1.4m.如果g取10m/s2,试计算:
(1)水滴下落到达窗台时的速度大小;
(2)水滴经过窗户的时间.