如图,平行四边形 中,
中,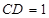 ,
, ,且
,且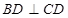 ,正方形
,正方形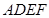 所在平面和平面
所在平面和平面 垂直,
垂直, 分别是
分别是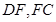 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证: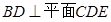 ;
;
(3)求三棱锥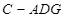 的体积.
的体积.
(本小题满分13分)已知函数
 .
.
(1)求函数 的最小正周期和最大值;
的最小正周期和最大值;
(2)在给出的直角坐标系中,画出函数 在区间
在区间 上的图象.
上的图象.
(3)设0<x< ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围.
(本小题满分12分)如图所示, 中,
中, ,
, ,
, ,
,
(1)试用向量 ,
, 来表示
来表示 .
.
(2)AM交DN于O点,求AO:OM的值.
(本小题满分12分)
已知函数f(x)=x2+(2+lga)x+lgb,f(-1)=-2.
(1)求a与b的关系式;
(2)若f(x)≥2x恒成立,求a、b的值.
(本小题满分12分)
已知 ,
, ,
,
(1)求 ;
;
(2)求 的值.
的值.
本小题满分12分)
(1)若 log2 [log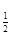 (log2 x)]=0,求x。;
(log2 x)]=0,求x。;
(2)若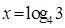 ,求
,求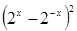 的值。
的值。