已知函数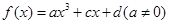 是R上的奇函数,当
是R上的奇函数,当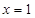 时
时 取得极值
取得极值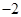 .
.
(I)求 的单调区间和极大值
的单调区间和极大值
(II)证明对任意
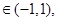 不等式
不等式 恒成立.
恒成立.
(本小题满分14分)
椭圆C的中心为坐标原点O,焦点在y轴上,离心率e = ,椭圆上的点到焦点的最短距离为1-, 直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且 .
.
⑴求椭圆方程;
⑵求m的取值范围.
(本小题满分12分
在 中,角
中,角 所对的边分别为
所对的边分别为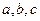 ,且满足
,且满足 ,
,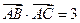
(I)求 的面积;
的面积;
(II)若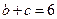 ,求
,求 的值
的值
(本小题满分12分)
等比数列{ }的前n 项和为
}的前n 项和为 ,已知
,已知 ,
, ,
, 成等差数列
成等差数列
(1)求{ }的公比q
}的公比q
(2)若 -
- =3,求
=3,求
(本小题满分10分
已知在 的展开式中,前三项的系数成等差数列
的展开式中,前三项的系数成等差数列
⑴求
⑵求展开式中的常数项
⑶求展开式中系数最大的项
(本小题满分10分
旅游公司为3个旅游团提供甲、乙、丙、丁4条旅游线路,每个旅游团任选其中一条
(Ⅰ)求3个旅游团选择3条不同的线路的概率
(Ⅱ)求选择甲线路旅游团数的分布列、期望E 及方差
及方差